

分析 (1)只要证明△AEH≌△BFE.推出BF=AE=2,由△MGF≌△BFE,推出△MGF≌△AEH,求出FC、GM即可解决问题.
(2)如图2,过点G作GM⊥BC,垂足为M,连接HF,根据S△GFC=$\frac{1}{2}$FC•GM,计算即可.
解答 解:(1)如图1,过点G作GM⊥BC,垂足为M.
由矩形ABCD可知:∠A=∠B=90°,
由正方形EFGH可知:
∠HEF=90°,EH=EF,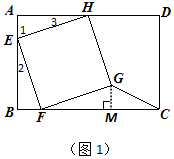
∴∠1+∠2=90°,
又∠1+∠3=90°,
∴∠3=∠2,
∴△AEH≌△BFE.
∴BF=AE=2,
同理可证:△MGF≌△BFE,
∴△MGF≌△AEH,
∴GM=AE=2,
又 FC=BC-BF=12-2=10,
∴S△GFC=$\frac{1}{2}$FC•GM=$\frac{1}{2}$×10×2=10.
(2)如图2,过点G作GM⊥BC,垂足为M,连接HF.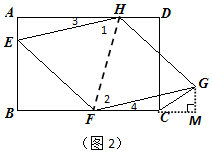
由矩形ABCD得:AD∥BC,
∴∠AHF=∠HFM,
由菱形EFGH得:EH∥FG,EH=FG,
∴∠1=∠2,
∴∠3=∠4,
又∠A=∠M=90°,EH=FG,
∴△MGF≌△AEH,
∴GM=AE=2,
又 BF=x,∴FC=12-x,
∴S△GFC=$\frac{1}{2}$FC•GM=$\frac{1}{2}$(12-x)•2=12-x,
即:S=12-x,
定义域:$0≤x≤4\sqrt{7}$.
点评 本题考查正方形的性质、矩形的性质、菱形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | x>4,x≤1 | B. | x<4,x≥-1 | C. | x>4,x>-1 | D. | x≤4,x>-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
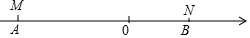 如图,点A、B在数轴上表示的数分别为-12和8,两只蚂蚁M、N分别从A、B两点同时出发,相向而行.M的速度为2个单位长度/秒,N的速度为3个单位长度/秒.
如图,点A、B在数轴上表示的数分别为-12和8,两只蚂蚁M、N分别从A、B两点同时出发,相向而行.M的速度为2个单位长度/秒,N的速度为3个单位长度/秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
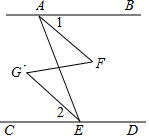 如图,已知∠BAE+∠AED=180°,∠1=∠2,那么∠F=∠G,为什么?
如图,已知∠BAE+∠AED=180°,∠1=∠2,那么∠F=∠G,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com