练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知0°＜＜90°，那么sin＋cos的值

    [　　]

    A．大于1　　　　B．等于1

    C．小于1　　　　D．大于或等于1

    答案：A
    解析：

    因为0＜a＜90°,则(sina+cosa)2=sin2a+cos2a+2sinacosa=1+2sinacosa＞1,所以(sina+cosa)2＞1,从而得sina+cosa＞1,故选A.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    23、如下图所示，已知△ABC，∠C=90°，AC=BC，按下列语句作图（尺规作图，保留痕迹，不必写作法）
    （1）①作∠B的平分线，交AC于D  ②过点D作DE⊥AB，垂足为E
    （2）根据以上所作图形，写出四组相等的线段．（不包括AC=BC）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2011•虹口区一模）已知0°＜α＜90°，如果sin（α-10°）=
    		3
    2
    ，那么α=
    70°
    70°
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

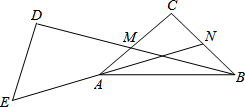    已知△ABC，∠C=90°，AC=BC．M为AC中点，延长BM到D，使MD=BM；N为BC中点，延长NA到E，使AE=NA，连接ED，求证：ED⊥BD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知△ABC，∠B=90°，按下列要求作图（尺规作图，不写作图步骤保留作图痕迹）
    （1）作∠C的角平分线与AB相交于D；在AC边上取一点E，使CE=CB，连接DE．
    （2）根据所作图形写出一对相等的线段和一对相等的锐角（不包括CE=CB，∠ECD=∠BCD）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    完成下列推理过程
    已知：如图，AB⊥BC于B，CD⊥BC于C，∠1=∠2．求证：BE∥CF．
    证明：∵AB⊥BC，CD⊥BC（已知）
    ∴∠1+∠3=90°，∠2+∠4=90°
    垂直定义
    垂直定义

    ∴∠1与∠3互余，∠2与∠4互余
    又∵∠1=∠2
    ∴∠3=∠4
    等角的余角相等
    等角的余角相等

    ∴BE∥CF
    内错角相等两直线平行
    内错角相等两直线平行
    ．

    查看答案和解析>>

    同步练习册答案