

⑴证明:∵正方形ABCD中,∠ABE=∠BCF=90。,AB=BC,
∴∠ABF+∠CBF=90。,
∵AE⊥BF,
∴∠ABF+∠BAE=90。,
∴∠BAE=∠CBF,
∴△ABE≌△BCF.
⑵解:∵正方形面积为3,
∴AB= ,
,
在△BGE 与△ABE 中,
∵∠GBE= ∠BAE, ∠EGB= ∠EBA=90。
∴△BGE ∽△ABE
∴ ,又BE=1,
,又BE=1,
∴AE2=AB2+BE2=3+1=4
∴ =
= =
= . (用其他方法解答仿上步骤给分).
. (用其他方法解答仿上步骤给分).
⑶解:没有变化
∵AB= ,BE=1,
,BE=1,
∴tan∠BAE=
 ,∠BAE=30°,
,∠BAE=30°,
∵AB′=AD,∠AB′E′=∠ADE'=90°,AE′公共,
∴Rt△ABE≌Rt△AB′E′≌Rt△ADE′,
∴∠DAE′=∠B′AE′=∠BAE=30°,
∴AB′与AE在同一直线上,即BF与AB′的交点是G,
设BF 与AE ′的交点为H,
则∠BAG= ∠HAG=30 °, 而∠AGB= ∠AGH=90 °,AG公共,
∴△BAG ≌△HAG,
∴S四边形GHE'B'=S△AB'E'-S△AGB=S△ABE- =S△BGE
=S△BGE
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
 (2012•益阳)已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(2012•益阳)已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(湖南益阳卷)数学(带解析) 题型:解答题
已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.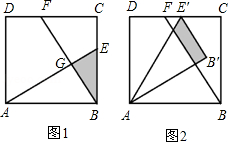
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(湖南益阳卷)数学(解析版) 题型:解答题
已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
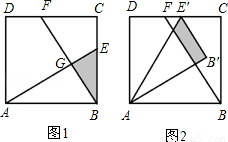
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB'E'(如图2),使点E落在CD边
上的点E'处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
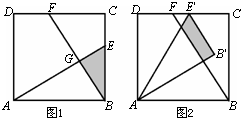 |
查看答案和解析>>
科目:初中数学 来源:2013年甘肃省武威十三中中考数学模拟试卷(一)(解析版) 题型:解答题
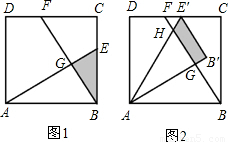
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com