
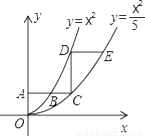
如图,平行于x轴的直线AC分别交抛物线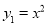 (x≥0)与
(x≥0)与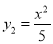 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则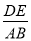 =________.
=________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:内蒙古巴彦淖尔市2017-2018学年九年级(上)期中数学试卷 题型:单选题
若关于x的一元二次方程方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是( )
A. k<5 B. k≥5,且k≠1 C. k≤5,且k≠1 D. k>5
C 【解析】试题解析:∵关于x的一元二次方程方程有实数根, ∴ 解得: 且k≠1. 故选C.查看答案和解析>>
科目:初中数学 来源:贵州铜仁伟才学校2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
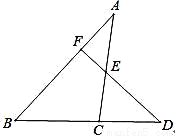
如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°.
(1)求∠B的度数.
(2)求∠ACD的度数.
查看答案和解析>>
科目:初中数学 来源:贵州铜仁伟才学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
用科学记数法表示0.00001032,下列正确的是( )
A. 0.1032×10-4 B. 1.032×103 C. 10.32×10-6 D. 1.032×10-5
D 【解析】根据对值小于1的正数也可以利用科学记数法表示方法(一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定)可得:0.00001032=1.032×10-5. 故选D.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区2017-2018学年九年级上册数学第一次月考试卷 题型:解答题
如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).
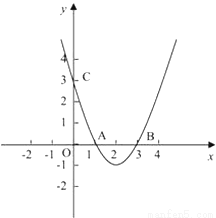
(1)求抛物线的函数关系式.
(2)将y=ax2+bx+c化成y=a(x﹣m)2+k的形式(请直接写出答案).
(3)若点D(3.5,m)是抛物线y=ax2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.
(1)y=x2﹣4x+3;(2). 【解析】试题分析:(1)将A、B、C三点坐标代入抛物线的解析式中,即可求出待定系数的值,从而确定该二次函数的解析式; (2)用配方法把一般式化为顶点式即可; (3)将D点坐标代入抛物线的解析式中,即可求出m的值;以AB为底,D点纵坐标的绝对值为高,即可求出△ABD的面积. 解析:(1)由已知得,解得, ∴y=x2﹣4x+3; ...查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区2017-2018学年九年级上册数学第一次月考试卷 题型:单选题
如图,已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1 , 0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )
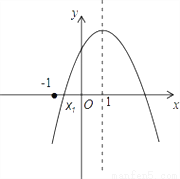
A. 1个 B. 2个 C. 3个 D. 4个
D 【解析】①抛物线对称轴在y轴的右侧,则a、b异号,即b>0. 抛物线与y轴交于正半轴,则c>0. ∵a<0, ∴abc<0. 故①错误; ②由图示知,当x=?3时,y<0,即9a?3b+c<0,故②正确; ③由图示知,x=?1时,y<0,即a?b+c<0, ∵x=?=1, ∴a=?b, ∴a?b+c=?b?b+c<0,即2c<3b,故...查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区2017-2018学年九年级上册数学第一次月考试卷 题型:单选题
已知(﹣1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=﹣2x2﹣8x+m上的点,则( )
A. y1<y2<y3 B. y3<y2<y1 C. y3<y1<y2 D. y2<y3<y1
C 【解析】试题分析:求出抛物线的对称轴,结合开口方向画出草图,根据对称性解答问题. 抛物线y=﹣2x2﹣8x+m的对称轴为x=﹣2,且开口向下,x=﹣2时取得最大值. ∵﹣4<﹣1,且﹣4到﹣2的距离大于﹣1到﹣2的距离,根据二次函数的对称性,y3<y1. ∴y3<y1<y2.查看答案和解析>>
科目:初中数学 来源:江西婺源县2016-2017学年第一学期期末考试七年级数学试卷 题型:填空题
35°48′32″+23°41′28″=___________°.
59.5 【解析】35°48′32″+23°41′28″=58°89′60″=59°30′=59.5°. 故答案为59.5.查看答案和解析>>
科目:初中数学 来源:2016-2017学年河北省张家口市桥东区七年级(下)期末数学试卷 题型:解答题
把下面的说理过程补充完整
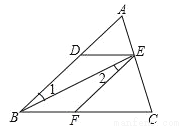
已知:如图,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
证明:∵DE∥BC(已知)
∴∠ADE= ( )
∵∠ADE=∠EFC(已知)
∴ = ( )
∴DB∥EF ( )
∴∠1=∠2 ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com