
 在Rt△ABC中,∠C=90°,
在Rt△ABC中,∠C=90°,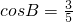 ,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么
,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么 =________.
=________.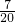
 =
= ,设BC=3x,则AB=4x,再根据勾股定理计算出AC=4x,在Rt△HBC中,根据余弦的定义可计算出BH=
,设BC=3x,则AB=4x,再根据勾股定理计算出AC=4x,在Rt△HBC中,根据余弦的定义可计算出BH= x,接着根据旋转的性质得CA′=CA=4x,CB′=CB,∠A′=∠A,所以根据等腰三角形的性质有B′H=BH=
x,接着根据旋转的性质得CA′=CA=4x,CB′=CB,∠A′=∠A,所以根据等腰三角形的性质有B′H=BH= x,则AB′=
x,则AB′= x,然后证明△ADB′∽△A′DC,再利用相似比可计算出B′D与DC的比值.
x,然后证明△ADB′∽△A′DC,再利用相似比可计算出B′D与DC的比值. 解:作CH⊥AB于H,如图,
解:作CH⊥AB于H,如图, =
= ,设BC=3x,则AB=5x,
,设BC=3x,则AB=5x, =4x,
=4x, =
= ,而BC=3x,
,而BC=3x, x,
x, x,
x, x,
x, =
= ,即
,即 =
= ,
, =
=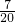 .
.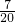 .
.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com