解:(1)∵点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=

的图象的两个交点,
∴m=-2,
∴反比例函数解析式为y=-

,
∴n=1,
∴点A(-2,1),
∵点A(-2,1),B(1,-2)是一次函数y=kx+b的图象上两点,
∴
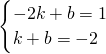
,
解得k=-1,b=-1,
故一次函数的解析式为y=-x-1;
(2)结合图象知:
当-2<x<0或x>1时,一次函数的值小于反比例函数的值;
(3)作点A关于x轴的对称点A′,连接BA′,延长交x轴于点C,则点C即为所求,

∵A(-2,1),
∴A′(-2,-1),
设直线A′B的解析式为y=mx+n,

,
解得m=-

,n=-

,
即y=-

x-

,
令y=0,x=-5,
则C点坐标为(-5,0),
当t=CB-CA有最大值,
则t=CB-CA=CB-CA′=A′B,
∴A′B=

=

.
分析:(1)根据点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=

的图象的两个交点,首先求出m的值,再求出n的值,最后列二元一次方程组求出一次函数解析式的系数;
(2)根据反比例函数和一次函数图象可以直接写出满足条件的x的取值范围;
(3)作点A关于x轴的对称点A′,连接BA′,延长交x轴于点C,则点C即为所求,求出A′点坐标,利用两点直线距离公式求出A′B的长度.
点评:本题主要考查反比例函数的综合题的知识点,解答本题的关键是熟练掌握求出一次函数以及反比例函数解析式的方法,解答第三问的时候需要熟练掌握对称点等相关知识,此题难度不大.

 如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=
如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点.
的图象的两个交点. 的图象的两个交点,
的图象的两个交点, ,
,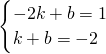 ,
,
 ,
, ,n=-
,n=- ,
, x-
x- ,
, =
= .
. 的图象的两个交点,首先求出m的值,再求出n的值,最后列二元一次方程组求出一次函数解析式的系数;
的图象的两个交点,首先求出m的值,再求出n的值,最后列二元一次方程组求出一次函数解析式的系数;

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2