
①S△GDC∶S△GEF=1∶4 ②S△GDC∶S△GAB=1∶9 ③S△GEF∶S△GAB=2∶3 ④S△GDC∶S四边形EFCD∶S四边形ABFE=1∶3∶5

A.1有 B.2有 C.3有 D.4有
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
 长线交于点G.
长线交于点G.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010-2011学年海南省三亚市实验中学八年级下学期期末考试数学 题型:解答题
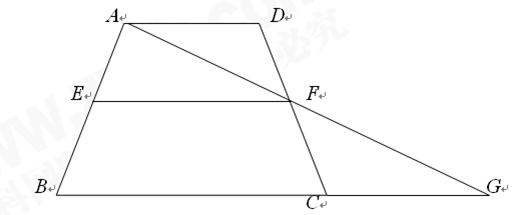
(11·曲靖)(9分)如图,在梯形ABCD中,AD∥BC,E、F分别是两腰AB、
DC的中点,AF、BC的延长线交于点G.
(1) 求证:△ADF≌△GCF.
(2) 类比三角形中位线的定义,我们把EF叫做梯形ABCD的中位线.阅读 填空:
填空:
在△ABG中:∵E中AB的中点
由(1)的结论可知F是AG的中点,
∴EF是△ABG的_______线
因此,可将梯形中位线EF与两底AD,BC的数量关系用文字语言表述为______________.
查看答案和解析>>
科目:初中数学 来源:云南省中考真题 题型:解答题
 BG=
BG= (BC+CG)
(BC+CG)  (______+________)
(______+________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com