
 西宁中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为
西宁中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为 米,在如图所示的坐标系中,这个喷泉的函数关系式是
米,在如图所示的坐标系中,这个喷泉的函数关系式是



 米,由此得到顶点坐标为(
米,由此得到顶点坐标为(  ,3),所以设抛物线的解析式为y=a(x-
,3),所以设抛物线的解析式为y=a(x- )2+3,而抛物线还经过(0,0),由此即可确定抛物线的解析式.
)2+3,而抛物线还经过(0,0),由此即可确定抛物线的解析式. 米,
米, ,3),
,3), )2+3,
)2+3, )2+3,
)2+3, )2+3.
)2+3.

科目:初中数学 来源: 题型:解答题
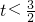 ,点P在BC上运动时,△PQD是以PD为一腰的等腰三角形,在直线BD上找一点E,在x轴上找一点F,是否存在以E,F,P,Q为顶点的平行四边形?若存在,求出E,F两点坐标;若不存在,请说明理由.
,点P在BC上运动时,△PQD是以PD为一腰的等腰三角形,在直线BD上找一点E,在x轴上找一点F,是否存在以E,F,P,Q为顶点的平行四边形?若存在,求出E,F两点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com