
 证明:如图所示,作∠DAO平分线交BC于K.
证明:如图所示,作∠DAO平分线交BC于K. ∠C=105°,
∠C=105°, ∠DAO
∠DAO (∠BAC-∠BAO)
(∠BAC-∠BAO) (∠BAC-60°)
(∠BAC-60°) ∠BAC=∠BAI=∠BEI.
∠BAC=∠BAI=∠BEI. ∠C=105°,可证得AK∥IE.由等腰△AOD可知DO丄AK,从而得出OI丄DE.由∠DIE=∠IDO,则OI=DE.
∠C=105°,可证得AK∥IE.由等腰△AOD可知DO丄AK,从而得出OI丄DE.由∠DIE=∠IDO,则OI=DE.

科目:初中数学 来源: 题型:
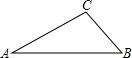 由于保管不慎,小明把一道数学题染上了污渍,变成了“如图,在△ABC中∠A=30°,tanB=
由于保管不慎,小明把一道数学题染上了污渍,变成了“如图,在△ABC中∠A=30°,tanB=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com