练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    正多边形的一个内角是120°，则这个正多边形的边数为(　　)

    A. 4 B. 8 C. 6 D. 12

    C 【解析】根据正多边的内角求出外角为180°-120°=60°，然后根据多边形的外角和为360°，可求其边数为360÷60°=6. 故选：C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：单选题

    如图，C是线段AB的中点，D是CB上一点，下列说法中错误的是(　　)

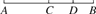
    A. CD＝AC－BD B. CD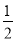＝BC C. CD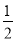＝AB－BD D. CD＝AD－BC

    B 【解析】根据CD=BC-BD和CD=AD-AC两种情况和AC=BC对各选项分析后即不难选出答案． 【解析】 ∵C是线段AB的中点， ∴AC=BC=AB， A、CD=BC-BD=AC-BD，正确； B、D不一定是BC的中点，故CD=BC不一定成立； C、CD=BC-BD=AB-BD，正确； D、CD=AD-AC=AD-BC，正确． 故选B． ...

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    已知点P（，1）关于原点的对称点在第四象限，则的取值范围是____________．

    【解析】试题解析: ∵P（，1关于原点对称的点在第四象限， ∴P点在第二象限， ∴a+1<0, 解得：a

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：填空题

    如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是__________. 

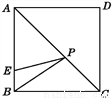
    10 【解析】试题分析：根据题意得：AE=6，AD=AB=8，根据正方形的性质可得点B关于AC的对称轴为点D，连接DE，DE与AC的交点就是点P，则DE==10．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：单选题

    如图，菱形ABCD中，AB=5，∠BCD=120°，则对角线AC的长是(　　)

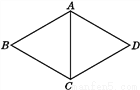
    A. 20 B. 15 C. 10 D. 5

    B 【解析】试题解析： 是菱形, 是等边三角形. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：解答题

    一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．

    （1）若从中任取一个球，求摸出球上的汉字刚好是“美”的概率；

    （2）甲从中任取一球，不放回，再从中任取一球，请用树状图或列表法，求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率．

    （1） P=；（2） P= 【解析】分析：（1）由一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球，除汉字不同之外，小球没有任何区别，直接利用概率公式求解即可求得答案； （2）首先根据题意列举出所有可能的结果与取出的两个球上的汉字恰能组成“美丽”或“南山”的情况，再利用概率公式即可求得答案． 本题解析： (1)∵有汉字“美”、“丽”、“南”、“山”...

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：填空题

    如图所示，一个长方体的长为4cm，宽为3cm，高为5cm．则长方体所有棱长的和为_______________；长方体的表面积为_______________ ．

    48cm 94cm2 【解析】长方体的长、宽、高分别为4cm，3cm，5cm， (1)这个长方体的棱长总和为4×(4+3+5)=48cm， 故长方体所有棱长的和为48cm. (2)表面积2×(4×3+4×5+3×5)=2×47=94cm². 故长方体的表面积为94cm². 故答案为：48cm;94cm².

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：解答题

    计算： +（﹣1）0﹣|﹣3|．

    1 【解析】试题分析：任何非零实数的零次幂为1，负数的绝对值等于它的相反数，9的算术平方根为3，然后进行有理数的加减法计算． 试题解析：【解析】 原式=3+1﹣3=1．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：单选题

    如图,已知的半径为10,弦,M是AB上任意一点,则线段OM的长可能是(    )

    A. 5 B. 7 C. 9 D. 11

    C 【解析】试题分析：过点O作OM′⊥AB，垂足为M，连接OA， ∵OM⊥AB，AB＝12 ∴AM′＝BM′＝6， 在Rt△OAM中，OM′＝＝8， ,所以8≤OM≤10， 故选C．

    查看答案和解析>>

    同步练习册答案