
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
 如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=$\frac{12}{13}$.
如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=$\frac{12}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-x-y)(x+y) | B. | (2x-y)(y-2x) | C. | (1-$\frac{1}{2}$x)(-1-$\frac{1}{2}$x) | D. | (3x+y)(x-3y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学建了一座竖直的电子屏幕HG,它的底部G点到地面BF的距离为3米,小明在CD处看电子屏幕的底部G点的仰角为30°,他在此处觉得视角不好,然后他后退了2米到AB处觉得好多了,此时他看电子屏幕的顶部H点的仰角为45°,已知小明眼睛到地面的距离为1.5米,求电子屏幕的宽度HG(结果精确到0.1,参考数据$\sqrt{2}≈$1.41,$\sqrt{3}$≈1.73)
某中学建了一座竖直的电子屏幕HG,它的底部G点到地面BF的距离为3米,小明在CD处看电子屏幕的底部G点的仰角为30°,他在此处觉得视角不好,然后他后退了2米到AB处觉得好多了,此时他看电子屏幕的顶部H点的仰角为45°,已知小明眼睛到地面的距离为1.5米,求电子屏幕的宽度HG(结果精确到0.1,参考数据$\sqrt{2}≈$1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
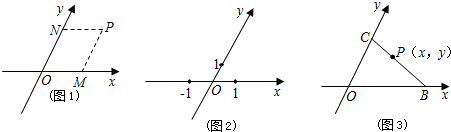
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com