练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

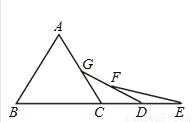
    如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=______。

    15° 【解析】试题分析：设∠E=x，根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解． 【解析】 设∠E=x， ∵DF=DE， ∴∠DFE=∠E=x， ∴∠CDG=∠E+∠DFE=2x， ∵CG=CD， ∴∠CDG=∠CGD=2x， ∴∠ACB=∠CDG+∠CGD=2x+2x=4x， ∵∠ACB=70°，...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：单选题

    如果代数式x2+4x+4的值是16，则x的值一定是（ ）

    A．-2 B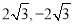． C．2，-6 D．30，-34

    C 【解析】试题分析： 由原题可列方程x2+4x+4=16， ∴x2+4x-12=0， ∴（x-2）（x+6）=0， ∴x=2或x=-6，故本题选C.

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：解答题

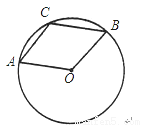
    已知如图所示，A，B，C是⊙O上三点，∠AOB=120°，C是 的中点，试判断四边形OACB形状，并说明理由．

    AOBC是菱形，理由见解析. 【解析】试题分析：连接OC，根据等边三角形的判定及圆周角定理进行分析即可． 试题解析：AOBC是菱形，理由如下： 连接OC， ∵C是 的中点 ∴∠AOC=∠BOC=×120°=60°， ∵CO=BO（⊙O的半径）， ∴△OBC是等边三角形， ∴OB=BC， 同理△OCA是等边三角形， ∴OA=AC， 又...

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：填空题

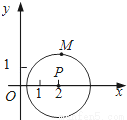
    如图，以点P（2，0）为圆心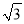， 为半径作圆，点M（a，b）是⊙P上的一点，则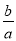的最大值是________ ．

    【解析】试题分析：当有最大值时，得出tan∠MOP有最大值，推出当OM与圆相切时，tan∠MOP有最大值，根据解直角三角形得出tan∠MOP=，由勾股定理求出OM，代入求出即可． 试题解析：当有最大值时，得出tan∠MOP有最大值， 也就是当OM与圆相切时，tan∠MOP有最大值， 此时tan∠MOP=， 在Rt△OMP中，由勾股定理得：OM=1， 则tan∠MOP=...

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：填空题

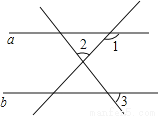
    如图所示，直线a∥b，∠1=130°，∠2=70°，求则∠3的度数．

    70° 【解析】试题分析：先根据三角形的外角的性质求得∠4的度数，再根据平行线的性质求解即可. ∵∠1＝130°，∠2＝70° ∴∠4＝130°-70°＝60° ∵a//b ∴∠3＝∠4＝60°.

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：填空题

    将一副常规的三角尺按如图方式放置，则图中∠AOB的度数为________

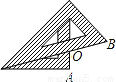
    105° 【解析】试题分析：根据直角三角尺的角度的特征即可求得结果. 由图可得∠AOB=60°+（90°-45°）=105°.

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：单选题

    如图所示，将三角板的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3的度数为（ ）

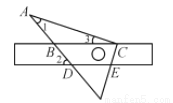
    A. 80° B. 50° C. 30° D. 20°

    D 【解析】试题分析：根据平行线的性质，得∠4=∠2=50°，再根据三角形的外角的性质∠3=∠4-∠1=50°-30°=20°．故答案选D．

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：单选题

    在Rt△ABC中,如果各边的长度同时扩大2倍，那么锐角A的正弦值和余弦值（   ）

    A. 都扩大2倍 B. 都缩小2倍 C. 都不变 D. 不能确定

    C 【解析】∵Rt△ABC中，若各边的长度同时都扩大2倍， ∴扩大后形成的三角形与原三角形相似， ∴锐角A的正弦与余弦的比值不变， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：安徽省宿州市（城西校区） 2017-2018学年九年级第一学期期中测试数学试卷 题型：填空题

    如图，边长为1的菱形ABCD中，∠DAB=60°．连结对角线AC，以AC为边作第二个菱形ACEF，使∠FAC=60°．连结AE，再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是_______．

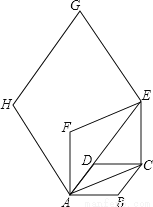
    （）n﹣1 【解析】试题分析：如图，连接DB于AC相交于M，根据菱形的性质可得AD=AB．AC⊥DB，又因∠DAB=60°， 所以△ADB是等边三角形，即可得DB=AD=1，再由菱形的性质和勾股定理可得BM=，AM=，从而得AC=，同理可得AE=AC=（）2，AG=AE=3=（）3，依此类推即可得第n个菱形的边长为（）n﹣1．

    查看答案和解析>>

    同步练习册答案