
如图,反比例函数 的图象经过点A(4,1),当
的图象经过点A(4,1),当 时,x的取值范围是( )
时,x的取值范围是( )

A.  或
或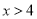 B.
B.  C.
C.  D.
D. 
科目:初中数学 来源:内蒙古乌兰察布分校2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
计算: 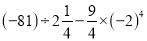
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:单选题
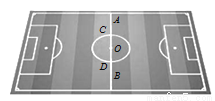
两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC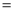 DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
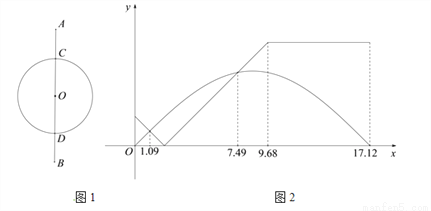
A. 小红的运动路程比小兰的长
B. 两人分别在1.09秒和7.49秒的时刻相遇
C. 当小红运动到点D的时候,小兰已经经过了点D
D. 在4.84秒时,两人的距离正好等于⊙O的半径
D 【解析】A选项,由题意结合图2可知,两人速度相同,同时出发,但小红比小兰先到达终点,因此小红的运动路程比小兰的短,所以A中说法错误; B选项,由图2可知在1.09秒时,两人距离C点的距离相等,但此时两人并没有相遇,所以B中说法错误; C选项,由题意结合图形分析可知,当小红运动到D点时,小兰还没有到达D点,所以C中说法错误; D选项,由图2可知,小红走完全程用时9.68秒...查看答案和解析>>
科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:解答题
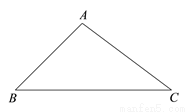
如图,在△ABC中,∠B为锐角, AB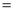
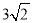 ,AC
,AC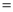 5,
5, 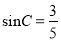 ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:填空题
如图,抛物线 的对称轴为
的对称轴为 ,点P,点Q是抛物线与x轴的两个交点,若点P的坐标为(4,0),则点Q的坐标为__________.
,点P,点Q是抛物线与x轴的两个交点,若点P的坐标为(4,0),则点Q的坐标为__________.

查看答案和解析>>
科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:单选题
在△ABC中,∠C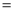 90°.若AB
90°.若AB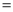 3,BC
3,BC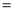 1,则
1,则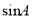 的值为( )
的值为( )
A. 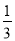 B.
B. 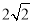 C.
C. 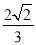 D.
D. 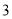
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
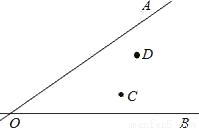
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
图中的图形中是常见的安全标记,其中是轴对称图形的是( )
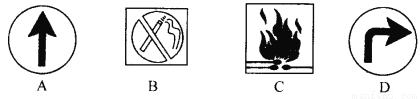
查看答案和解析>>
科目:初中数学 来源:2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型:单选题
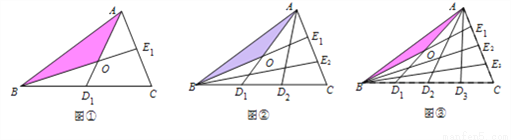
设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )
A.  B.
B.  C.
C. 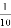 D.
D. 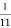
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com