解:(1)∵y=-

x+2分别交x轴,y轴于A,B两点,
∴A(4,0),B(0,2),
又∵抛物线y=-x
2+bx+c过A、B两点,
∴c=2,-16+4b+c=0,
∴b=

,c=2,
∴y=-x
2+

x+2;
(2)∵点M在y=-

x+2上,
设M(p,-

p+1),
∵MN∥y轴且N在y=-x
2+

x+2上,
∴N(p,-p
2+

p+2),
∴MN=-p
2+

p+2-(-

p+2)=-p
2+4p=-(p-2)
2+4,
∴p=2时,MN的最大值是4;
(3)在(2)的情况下,即p=2、MN=4时,
此时B(0,2),M(2,1),N(2,5),
①若BM是平行四边形的边,则BD=MN,
此时点D的坐标为(0,6)或(4,4);
②若BM是平行四边形的对角线,
设点D的坐标为(x,y),则(2+x,5+y)=(0+2,2+1),
解得:x=0,y=-2
此时点D的坐标为(0,-2).
综上可得:D
1(4,4);D
2(0,6);D
3(0,-2).
分析:(1)根据直线解析式求出点A、B的坐标,利用待定系数法可求出抛物线解析式;
(2)设M(p,-

p+1),根据MN∥y轴且N在y=-x
2+

x+2上,可得N(p,-p
2+

p+2),表示出MN的长度,利用配方法可求出MN的最大值,也可确定此时P的值;
(3)由(2)中求得的p的值,可得出M、N的坐标,分两种情况讨论,①BM是平行四边形的边,②BM是平行四边形的对角线,根据平行四边形的性质可得出点D的坐标.
点评:本题考查了二次函数的综合,综合考察的知识点较多,解答本题的关键是掌握平行四边形的性质,能根据已知三点坐标求出第四个顶点的坐标,此题难度较大.

 直线y=
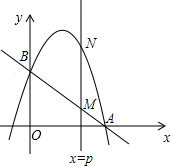
直线y= x+2分别交x轴、y轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
x+2分别交x轴、y轴于A、B两点,抛物线y=-x2+bx+c过A、B两点. x+2分别交x轴,y轴于A,B两点,
x+2分别交x轴,y轴于A,B两点, ,c=2,
,c=2, x+2;
x+2; x+2上,
x+2上, p+1),
p+1), x+2上,
x+2上, p+2),
p+2), p+2-(-
p+2-(- p+2)=-p2+4p=-(p-2)2+4,
p+2)=-p2+4p=-(p-2)2+4, p+1),根据MN∥y轴且N在y=-x2+
p+1),根据MN∥y轴且N在y=-x2+ x+2上,可得N(p,-p2+
x+2上,可得N(p,-p2+ p+2),表示出MN的长度,利用配方法可求出MN的最大值,也可确定此时P的值;
p+2),表示出MN的长度,利用配方法可求出MN的最大值,也可确定此时P的值;

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案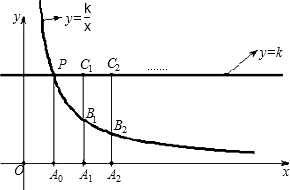 别作x轴的垂线,与双曲线y=
别作x轴的垂线,与双曲线y= A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.
A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.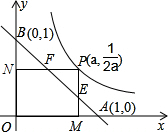 如图,P是函数y=
如图,P是函数y=