Question

某边防部接到情报，近海处有一可疑船只A正向公海方向行驶，边防部迅速派出快艇B追赶．在追赶过程中，设快艇B相对于海岸的距离为y₁(海里)，可疑船只A相对于海岸的距离为y₂(海里)，追赶时间为t(分钟)，图中l_A、l_B分别表示y₂、y₁与t之间的关系．结合图象回答下列问题：

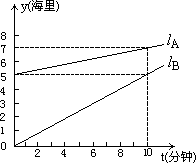
(1)请你根据图中标注的数据，分别求出y₁、y₂与t之间的函数关系式，并写出自变量的取值范围；

(2)15分钟内B能否追上A？说明理由；

(3)已知当A逃到离海岸12海里的公海时，B将无法对其进行检查．照此速度计算，B能否在A逃入公海前将其拦截？

Answer 1

答案：
解析：

(1)设lB∶y1=kt＋b，由目可知，lB经过点(0，0)和(10，5)，代入得，解方程组得 　　∴y1=t(t≥0)，同理可得1A∶y2=t＋5(t≥0)：(2)当t＝15时，y1=15×=，y2=×15＋5=8，可见y1＜y2，故15分钟内快艇B尚未追上可疑船只A 　　(3)，得t，所以快艇B追上可疑船只A在逃入公海前，快艇B能够追上A将其拦截．