
如果记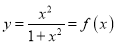 ,并且f(1)表示当
,并且f(1)表示当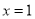 时y的值,即f(1)=
时y的值,即f(1)=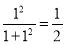 ;f(
;f(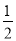 )表示当
)表示当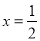 时y的值,即f(
时y的值,即f(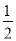 )=
)=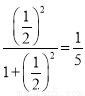 .那么
.那么
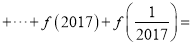 ______.
______.
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:单选题
已知A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A. 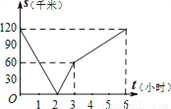 B.
B. 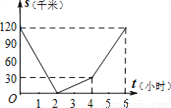
C. 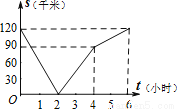 D.
D. 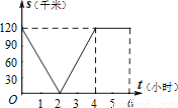
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:填空题
长为a、宽为b的矩形,它的周长为16,面积为12,则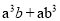 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
下列计算中,正确的是( )
A. 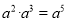 B.
B. 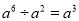
C. 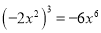 D.
D. 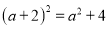
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:解答题
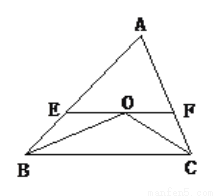
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F.
(1)判断△BEO的形状,并说明理由.
(2)若AB=5cm,AC=4cm,求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
若点A(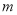 ,7)与点B(8,
,7)与点B(8, 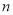 )关于
)关于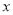 轴对称,则
轴对称,则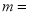 ________________.
________________.
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
如图,点P是∠BAC的平分线AD上一点,PE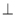 AC于点E.已知∠BAC =60° ,PA=6,则PE长是( )
AC于点E.已知∠BAC =60° ,PA=6,则PE长是( )
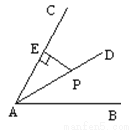
A. 3 B. 4 C. 5 D. 6
A 【解析】试题解析:过P作PF⊥AB于F, ∵点P是∠BAC的平分线AD上一点,PE⊥AC,PF⊥AB,PE=3, ∴PE=PF=3, 故选A.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:填空题
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为_____度.
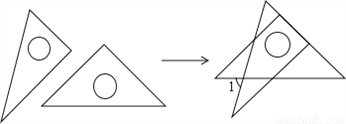
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:解答题
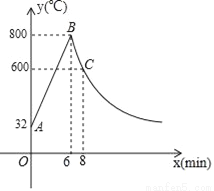
如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com