练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

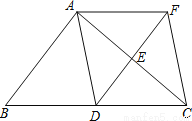
    如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于F点，连接AD、CF．

    （1）求证：四边形ADCF是平行四边形；

    （2）当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．

    （1）证明见解析；（2）等腰直角三角形. 【解析】试题分析： （1）先证四边形ABDF是平行四边形，再证结论； （2）由四边形ADCF是正方形来证明△ABC是等腰直角三角形. 试题解析： （1）证明：∵点D、E分别是边BC、AC的中点，∴DE∥AB， ∵AF∥BC，∴四边形ABDF是平行四边形，∴AF=BD，则AF=DC=AD， ∵AF∥BC，∴四边形AD...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年云南省腾冲市七年级上学期期末考试数学试卷 题型：解答题

    当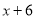与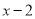互为相反数时，求下列代数式的值：（先化简再求值）.

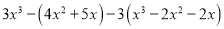    6 【解析】试题分析：先求出的值，对原式去括号，合并同类项，再把的值代入求值即可. 试题解析： 与互为相反数, . . 原式. . 当时， 原式= .

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年广东省八年级12月月考数学试卷 题型：单选题

    若y=(m一1 ) 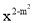是正比例函数，则m的值为 ( )

    A. 1 B. -1 C. 1或-1 D. 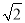或-

    B 【解析】【解析】 根据正比例函数的定义，可得2﹣m2=1，m﹣1≠0，∴m=﹣1．故选B．

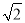
    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型：单选题

    计算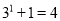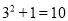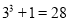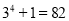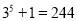： ， ， ， ， ， ，归纳各计算结果中的个位数字的规律，猜测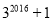的个位数字是（ ）

    A. 0 B. 2 C. 4 D. 8

    B 【解析】∵2016÷4=504, ∴即 +1的个位数字与的个位数字相同为2. 所以B选项是正确的.

    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型：单选题

    下列合并同类项正确的是（ ）

    A. 3x＋3y =6xy B. 7x2－5x2=2 C. 4＋5ab=9ab D. 2m2n－m2n=m2n

    D 【解析】A. 3x＋3y ，不是同类项不能合并,故错误; B. 7x2－5x2=2≠2，故错误; C. 4＋5ab=9ab，不是同类项不能合并,故错误; D. 2m2n－m2n=m2n，故正确. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：解答题

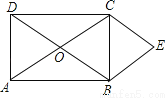
    平行四边形ABCD的对角线AC和BD交于O点，分别过顶点B，C作两对角线的平行线交于点E，得平行四边形OBEC．

    （1）如果四边形ABCD为矩形（如图），四边形OBEC为何种四边形？请证明你的结论；

    （2）当四边形ABCD是　 　 形时，四边形OBEC是正方形．

    （1）证明见解析；（2）正方 【解析】（1）根据矩形的性质：两条对角线相等且互相平分，即可得到结论；（2）根据正方形的性质：对角线相等且互相垂直平分，即可得到结论. 【解析】 （1）四边形OBEC是菱形．理由如下： ∵BE∥OC，CE∥OB， ∴四边形OBEC为平行四边形． 又∵四边形ABCD是矩形， ∴OC=AC; OB=BD；AC=BD ∴OC=OB...

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：单选题

    下列命题中，正确的是（　　）

    A. 四边相等的四边形是正方形

    B. 四角相等的四边形是正方形

    C. 对角线垂直的平行四边形是正方形

    D. 对角线相等的菱形是正方形

    D 【解析】试题分析：根据正方形的判定：对角线相等且互相垂直平分的四边形是正方形，对各个选项进行分析． 【解析】 A，错误，四边相等的四边形也可能是菱形； B，错误，矩形的四角相等，但不是正方形； C，错误，对角线垂直的平行四边形是菱形； D，正确，符合正方形的判定； 故选D．

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：单选题

    如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）

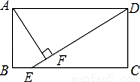
    A. △AFD≌△DCE B. AF=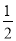AD C. AB=AF D. BE=AD﹣DF

    C 【解析】A．由矩形ABCD，AF⊥DE可得∠C=∠AFD=90°，AD∥BC，∴∠ADF=∠DEC． 又∵DE=AD，∴△AFD≌△DCE（AAS），故A正确； B．∵∠ADF不一定等于30°，∴直角三角形ADF中，AF不一定等于AD的一半，故B错误； C．由△AFD≌△DCE，可得AF=CD，由矩形ABCD，可得AB=CD，∴AB=AF，故C正确； D．由△AF...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省鸡西市虎林市八五八农场学校2018届九年级（上）期中考试数学试卷 题型：单选题

    如图已知在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE、PF分别交AB和AC于点E、F，给出以下五个结论正确的个数有（　　）

    ①AE=CF②∠APE=∠CPF ③△BEP≌△AFP④△EPF是等腰直角三角形⑤当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合），S四边形AEPF=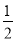S△ABC．

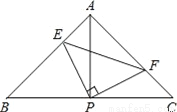
    A. 2 B. 3 C. 4 D. 5

    D 【解析】试题分析：∵AB＝AC，∠BAC＝90°，点P是BC的中点， ∴AP⊥BC，AP＝PC，∠EAP＝∠C＝45°， ∴∠APF＋∠CPF＝90°， ∵∠EPF是直角， ∴∠APF＋∠APE＝90°， ∴∠APE＝∠CPF，故②正确； 在△APE和△CPF中， ， ∴△APE≌△CPF（ASA）， ∴AE＝CF，故①正确； ...

    查看答案和解析>>

    同步练习册答案