
如图,在△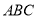 中,
中, 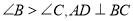 ,垂足为
,垂足为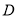 ,
, 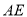 平分
平分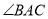 .已知
.已知 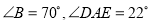 ;求
;求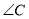 的度数.
的度数.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源:内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型:填空题
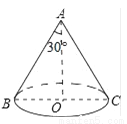
如图,已知圆锥的高为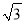 ,高所在直线与母线的夹角为30°,圆锥的侧面积为_____.
,高所在直线与母线的夹角为30°,圆锥的侧面积为_____.
查看答案和解析>>
科目:初中数学 来源:湖北省元月联合测试数学试卷 题型:解答题
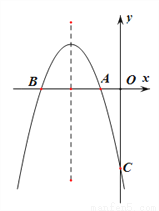
如图,已知抛物线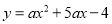 交
交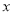 轴于点
轴于点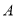 、点
、点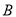 ,交
,交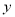 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求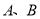 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点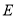 异于
异于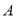 ,且
,且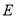 在对称轴右侧),直线
在对称轴右侧),直线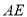 交对称轴于N,
交对称轴于N,
直线BE交对称轴于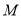 ,对称轴交
,对称轴交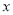 轴于
轴于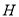 ,试确定
,试确定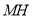 、
、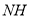 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源:湖北省元月联合测试数学试卷 题型:单选题
将抛物线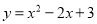 向左平移2个单位,再向上平移1个单位,得到的抛物线的解析式为( )
向左平移2个单位,再向上平移1个单位,得到的抛物线的解析式为( )
A. 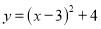 B.
B. 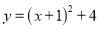 C.
C. 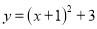 D.
D. 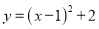
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期八年级期末统一考试数学试卷 题型:解答题
在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.如:在图1中,若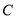 是
是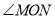 的平分线
的平分线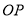 上一点,点
上一点,点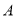 在
在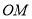 上,此时,在
上,此时,在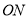 截取
截取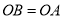 ,连接
,连接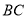 ,根据三角形全等的判定
,根据三角形全等的判定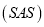 ,容易构造出全等三角形⊿
,容易构造出全等三角形⊿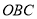 和⊿
和⊿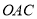 ,参考上面的方法,解答下列问题:
,参考上面的方法,解答下列问题:
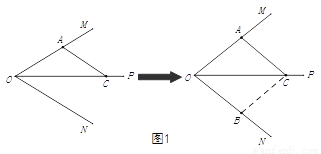
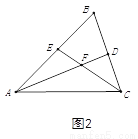
如图2,在非等边⊿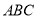 中,
中, 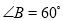 ,
, 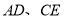 分别是
分别是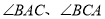 的平分线,且
的平分线,且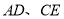 交于点
交于点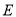 .求证:
.求证: 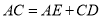 .
.
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期八年级期末统一考试数学试卷 题型:填空题
若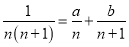 ,对于任意正整数
,对于任意正整数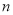 都成立,则
都成立,则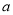 = ,
= , 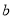 = ;根据上面的式子,计算
= ;根据上面的式子,计算 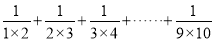 = .
= .
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期八年级期末统一考试数学试卷 题型:单选题
已知甲车行驶30千米与乙车行驶40千米所用时间相同,并且乙车每小时比甲车多行驶15千米.若设甲车的速度为x千米/时,依题意列方程正确的是( )
A.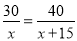 B.
B.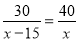
C.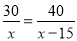 D.
D.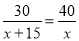
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼和浩特市九年级(下)期中数学试卷 题型:填空题
一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图扇形的圆心角是 .
180° 【解析】试题解析:设底面圆的半径为r,侧面展开扇形的半径为R,扇形的圆心角为n度. 由题意得S底面面积=πr2, l底面周长=2πr, S扇形=2S底面面积=2πr2, l扇形弧长=l底面周长=2πr. 由S扇形=l扇形弧长×R得2πr2=×2πr×R, 故R=2r. 由l扇形弧长=得: 2πr= 解得n=180°.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:解答题
将函数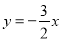 的图像向上平移
的图像向上平移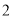 个单位长度,平移后的图像经过点
个单位长度,平移后的图像经过点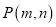 .若点
.若点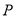 位于第一象限,求实数
位于第一象限,求实数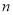 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com