练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    把0.697按四舍五入法精确到0.01的近似值是 ．

    0．70 【解析】试题分析：求一个数的近似数利用四舍五入法，需要看精确度的后一位，然后利用四舍五入的方法进行计算.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：天津市宝坻区口东镇2018届九年级12月月考数学试卷 题型：单选题

    下列图形是中心对称图形的是（　　）

    A. B. C. D.

    C 【解析】在同一平面内，如果把一个图形绕某一点旋转180度，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．由此可得选项A不是中心对称图形；选项B不是中心对称图形；选项C是中心对称图形；选项D不是中心对称图形．故选C．

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区联盟校2018届九年级（上）期中数学试卷 题型：单选题

    函数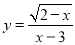 的自变量x的取值范围是（　　）

    A. x≤2 B. x≥2且x≠3 C. x≥2 D. x≤2且x≠3

    A 【解析】试题解析：根据题意得：2-x≥0且x-3≠0， 解得：x≤2且x≠3， 自变量的取值范围x≤2， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：北京师范大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    下面计算是否正确？若不正确，指出错因，并予以改正

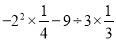
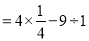
    =1-9

    =-8

    -2 【解析】试题分析：本题考查了有理数的混合运算，按照先算乘方（开方），再算乘除，最后算加减，同一级运算从左往右一次计算. 【解析】 不正确，一是乘方运算错误，二是运算顺序错误. 原式=

    查看答案和解析>>

    科目：初中数学 来源：北京师范大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    若=0是关于x的一元一次方程，则m=_______.

    -1 【解析】由题意得 且 ， ∴.

    查看答案和解析>>

    科目：初中数学 来源：北京师范大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    下列去（添）括号做法正确的有

    A. x-（y-z）=x-y-z B. -（x-y+z）=-x-y-z

    C. x+2y-2z=x-2（z-y） D. –a+c+d+b=-（a+b）+（c+d）

    C 【解析】A. ∵x-（y-z）=x-y+z ，故不正确； B. ∵ -（x-y+z）=-x+y-z ，故不正确； C. ∵x+2y-2z=x-2（z-y），故正确； D. ∵ –a+c+d+b=-（a-b）+（c+d），故不正确； 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：解答题

    已知：如图，OC是∠AOB的平分线．

    (1)当∠AOB＝60°时，求∠AOC的度数；

    (2)在(1)的条件下，∠EOC＝90°，请在图中补全图形，并求∠AOE的度数；

    (3)当∠AOB＝α时，∠EOC＝90°，直接写出∠AOE的度数．(用含α的代数式表示)

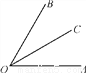
    (1) 30°；(2) 120°或60°；(3)90°＋或90°－. 【解析】试题分析：（1）直接由角平分线的意义得出答案即可； （2）分两种情况：OE在OC的上面，OE在OC的下面，利用角的和与差求得答案即可； （3）类比（2）中的答案得出结论即可． 试题解析：【解析】 （1）∵OC是∠AOB的平分线（已知），∴∠AOC=∠AOB，∵∠AOB=60°，∴∠AOC=30°...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：单选题

    下列语句正确的是（　　）

    A．画直线AB=10厘米

    B．画直线l的垂直平分线

    C．画射线OB=3厘米

    D．延长线段AB到点C，使得BC=AB

    D 【解析】 【解析】 A、直线无限长；B、直线没有中点，无法画垂直平分线；C、射线无限长；D、延长线段AB到点C，使得BC=AB，正确．故本题选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：解答题

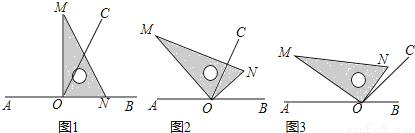
    （2015秋•乐亭县期中）点O为直线AB上一点，过点O作射线OC，使∠BOC=65°，将一直角三角板的直角顶点放在点O处．

    （1）如图①，将三角板MON的一边ON与射线OB重合时，则∠MOC= ；

    （2）如图②，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的角平分线，求旋转角∠BON和∠CON的度数；

    （3）将三角板MON绕点O逆时针旋转至图③时，∠NOC=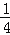∠AOM，求∠NOB的度数．

    （1）25°；（2）25°；（3）70°． 【解析】 试题分析：（1）根据∠MON和∠BOC的度数可以得到∠MON的度数． （2）根据OC是∠MOB的角平分线，∠BOC=65°可以求得∠BOM的度数，由∠NOM=90°，可得∠BON的度数，从而可得∠CON的度数． （3）由∠BOC=65°，∠NOM=90°，∠NOC=∠AOM，从而可得∠NOC的度数，由∠BOC=65°，从...

    查看答案和解析>>

    同步练习册答案