练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，∠POQ＝，边长为2cm的正方形ABCD的顶点B在OP上，C在OQ上，且∠OBC＝，分别求点A、D到OP的距离．

    答案：
    解析：

    过A作AE⊥OP于E，则∠BAE＝，∴BE＝AB＝1cm，∴AE＝cm．∴A到OP距离为cm　　过A作AF∥OP交CD于F，过D作DH⊥AF于H，则∠DAH＝，∵AD＝2cm，∴DH＝1cm　　∴D到OP的距离为＋1＝＋1cm．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省温州市实验中学2012届九年级上学期月考数学试题 题型：044

    将正方形ABCD绕中心O顺时针旋转角α得到正方形A1B1C1D1，如图所示．

    (1)当α＝45°时(如下图)，若线段OA与边A1D1的交点为E，线段OA1与AB的交点为F，可得下列结论成立①△EOP≌△FOP；②PA＝PA1，试选择一个证明．

    (2)当0°＜α＜90°时，第(1)小题中的结论PA＝PA1还成立吗？如果成立，请证明；如果不成立，请说明理由．

    (3)在旋转过程中，记正方形A1B1C1D1与AB边相交于P，Q两点，探究∠POQ的度数是否发生变化？如果变化，请描述它与α之间的关系；如果不变，请直接写出∠POQ的度数．

    查看答案和解析>>

    科目：初中数学 来源：中考备考专家数学(第二版) 题型：044

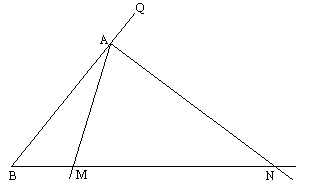
    如图，已知A为∠POQ的边OQ上一点，以A为顶点的∠MAN的两边分别交OP于M、N两点，且∠MAN＝∠POQ＝α(α为锐角)．当∠MAN以点A为旋转点中心，AM边从与AO重合的位置开始，按逆时针方向旋转(∠MAN保持不变)时，M、N在射线OP上同时以不同的速度向右平行移动．设OM＝x，ON＝y(y＞x≥0)，△AOM面积为S，若cosα、OA是方程2z2－5z＋2＝0的两个根．

    (1)当∠AMN旋转(即∠OAM＝)时，求点N移动的距离；

    (2)求证：AN2＝ON·MN；

    (3)求y与x之间的函数关系式及自变量x的取值范围；

    (4)试写出S随x变化的函数关系式，并确定S的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：1＋1轻巧夺冠优化训练九年级数学上 北京课改版 题型：044

    如图，∠POQ＝90°，边长为2 cm的正方形ABCD的顶点B在OP上，C在OQ上，且∠OBC＝30°，分别求点A、D到OP的距离．

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　(下册)　(配华东师大版新课标) 华东师大版新课标 题型：044

    如图所示，已知A为∠POQ的边OQ上一点，以A为顶点的∠MAN的两边分别交射线OP于M，N两点，且∠MAN＝∠POQ＝α(α为锐角)．当∠MAN以点A为旋转中心，AM从与AO重合的位置开始，按逆时针方向旋转(∠MAN保持不变)时，M，N两点在射线OP上同时以不同的速度向右平行移动，设OM＝x，ON＝y(y＞x≥0)，△AOM的面积为S，若cosα，OA是方程2z2－5z＋2＝0的两个根．

    (1)当∠MAN旋转30°(即∠OAM＝30°)时，求点N移动的距离；

    (2)求证AN2＝ON·MN；

    (3)求y与x之间的函数关系式及自变量x的取值范围；

    (4)试写出S随x变化的函数关系式，并确定S的取值范围．

    查看答案和解析>>

    同步练习册答案