
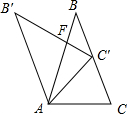
 如图△ABC,AB=BC,将△ABC绕点A逆时针旋转一定的角度得到△AB′C′,当点C′恰好能落在BC的中点处时,B′C′与AB交于点F,若AC=2,则C′F的长为________.
如图△ABC,AB=BC,将△ABC绕点A逆时针旋转一定的角度得到△AB′C′,当点C′恰好能落在BC的中点处时,B′C′与AB交于点F,若AC=2,则C′F的长为________.
 ,得到AB=BC=B′C′=B′A=2
,得到AB=BC=B′C′=B′A=2 ,BC′=
,BC′= ,再证明△BFC′∽△∠B′FA,则BF:B′F=FC′:FA=BC′:B′A=
,再证明△BFC′∽△∠B′FA,则BF:B′F=FC′:FA=BC′:B′A= :2
:2 =1:2,设BF=x,FC′=y,则B′F=2x,FA=2y,利用B′F+FC′=B′C′=2
=1:2,设BF=x,FC′=y,则B′F=2x,FA=2y,利用B′F+FC′=B′C′=2 ,BF+FA=2
,BF+FA=2 ,可得到关于x与y的方程组,解方程组即可.
,可得到关于x与y的方程组,解方程组即可. ,
, ,BC′=
,BC′= ,
, :2
:2 =1:2,
=1:2, ,BF+FA=2
,BF+FA=2 ,
,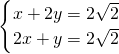 ,
,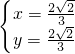 ,
, .
. .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图△ABC,AB=BC,将△ABC绕点A逆时针旋转一定的角度得到△AB′C′,当点C′恰好能落在BC的中点处时,B′C′与AB交于点F,若AC=2,则C′F的长为
如图△ABC,AB=BC,将△ABC绕点A逆时针旋转一定的角度得到△AB′C′,当点C′恰好能落在BC的中点处时,B′C′与AB交于点F,若AC=2,则C′F的长为2
| ||
| 3 |
2
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012年河南省中考模拟试题数学卷 题型:解答题
(本题8分)如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.
 |
查看答案和解析>>
科目:初中数学 来源:2012年河南省招数学模拟试卷 题型:解答题
如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com