练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．平行四边形ABCD中，对角线AC和BD交于点O，若AC=8，BD=6，设AB长为x，则x的取值范围是1＜AB＜7．

    分析 由平行四边形ABCD中，对角线AC和BD交于点O，若AC=8，BD=6，根据平行四边形的对角线互相平分，即可求得OA与OB的值，又由三角形的三边关系，即可求得答案．

    解答 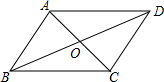解：∵四边形ABCD是平行四边形，
    ∴OA=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4，OB=$\frac{1}{2}$BD=$\frac{1}{2}$×6=3，
    ∴4-3＜AB＜4+3，
    ∴1＜AB＜7．
    故答案为：1＜AB＜7．

    点评 此题考查了平行四边形的性质以及三角形三边关系．注意平行四边形的对角线互相平分是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．已知4x2m-5-5yn+3=1是关于x、y的二元一次方程，则m=3；n=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．解分式方程
    （1）$\frac{x+1}{{{x^2}-5}}=\frac{1}{x}$
    （2）$\frac{1}{x-2}=\frac{1-x}{2-x}-3$．

    查看答案和解析>>

    同步练习册答案