
 将一副角板如图放置,则上、下两块三角板的面积S1:S2=________.
将一副角板如图放置,则上、下两块三角板的面积S1:S2=________.
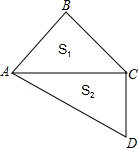 解:设两个三角板重合的边CA=x,
解:设两个三角板重合的边CA=x, ,
, AB•CB=
AB•CB= ×
× •
• =
= x2,
x2, x,
x, •AC•CD=
•AC•CD= •x•
•x• x=
x= x2,
x2, x2:
x2: x2=
x2= :2,
:2, :2.
:2.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com