
 解:(1)是定值.
解:(1)是定值. a•PE,S△CPB=
a•PE,S△CPB= a•PF,S△APC=
a•PF,S△APC= a•PG,
a•PG, a•PE+
a•PE+ a•PF+
a•PF+ a•PG,
a•PG, a•PE+
a•PE+ a•PF+
a•PF+ a•PG=S,
a•PG=S,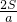 ,为定值.
,为定值.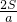 ,为定值.
,为定值.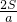 .
.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市黄浦区数学学业考试模拟试卷 题型:解答题
(8分)阅读下列材料
将图1的平行四边形用一定方法可分割成面积相等的八个四边形,如图2,再将图2中的八个四边形适当组合拼成两个面积相等且不全等的平行四边形.(要求:无缝隙且不重叠)
请你参考以上做法解决以下问题:
(1)将图4的平行四边形分割成面积相等的八个三角形;
(2)将图5的平行四边形用不同于(1)的分割方案,分割成面积相等的八个三角形,再将这八个三角形适当组合拼成两个面积相等且不全等的平行四边形,类比图2,图3,用数字1至8标明.

(3)设每个小格点正方形的边长为1,请你直接写出在(2)中拼成的两个不全等的平行四
边形的周长。
查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市考模拟数学试卷 题型:解答题
(8分)阅读下列材料
将图1的平行四边形用一定方法可分割成面积相等的八个四边形,如图2,再将图2中的八个四边形适当组合拼成两个面积相等且不全等的平行四边形.(要求:无缝隙且不重叠)
请你参考以上做法解决以下问题:
(1)将图4的平行四边形分割成面积相等的八个三角形;
(2)将图5的平行四边形用不同于(1)的分割方案,分割成面积相等的八个三角形,再将这八个三角形适当组合拼成两个面积相等且不全等的平行四边形,类比图2,图3,用数字1至8标明.

(3)设每个小格点正方形的边长为1,请你直接写出在(2)中拼成的两个不全等的平行四
边形的周长。
查看答案和解析>>
科目:初中数学 来源:2010年上海市普陀区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com