
在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.

(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是________;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是________;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
|
解:(1)四边形EGFH是平行四边形 1分 证明:∵□ABCD的对角线AC、BD交于点O. ∴点O是□ABCD的对称中心. ∴EO=FO,GO=HO. ∴四边形EGFH是平行四边形 4分 (2)菱形 5分 (3)菱形 6分 (4)四边形EGFH是正方形 7分 证明:∵AC=BD,∴□ABCD是矩形.又∵AC⊥BD,∴□ABCD是菱形. ∴□ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC. ∵EF⊥GH,∴∠GOF=90°.∴∠BOG=∠COF. ∴△BOG≌△COF.∴OG=OF,∴GH=EF 9分 由(1)知四边形EGFH是平行四边形,又∵EF⊥GH,EF=GH. ∴四边形EGFH是正方形 10分 |


科目:初中数学 来源: 题型:
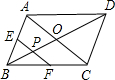 如图,在?ABCD中,AC=6,BD=8,P是对角线BD上的任意一点,过点P作EF∥AC,与?ABCD的两条边分别交于点E,F.设BP=x,EF=y,则下面能大致反映y与x之间关系的图象为( )
如图,在?ABCD中,AC=6,BD=8,P是对角线BD上的任意一点,过点P作EF∥AC,与?ABCD的两条边分别交于点E,F.设BP=x,EF=y,则下面能大致反映y与x之间关系的图象为( )A、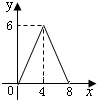 | B、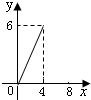 | C、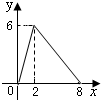 | D、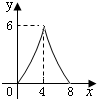 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com