
如图,E是正方形ABCD的边BC的中点,F是CD上一点,DF=3CF.

求证:AE⊥EF.
|
证明:连结AF. 设CF=x,则DF=3x,CD=4x. ∵E是BC的中点, ∴AB=4x,BE=EC=2x. 在Rt△ABE中, AE2=AB2+BE2=16x2+4x2=20x2. 在Rt△ADF中,(勾股定理) AF2=AD2+DF2=16x2+9x2=25x2. 在Rt△ECF中, EF2=EC2+CF2=4x2+x2=5x2. ∴AE2+EF2=20x2+5x2=25x2=AF2, ∴△AEF是直角三角形,且∠AEF= 即AE⊥EF.(勾股定理的逆定理,常用来证明线段垂直) |
|
点评:此题是勾股定理逆定理的典型应用,通过“计算”的方法,“算”出两条直线互相垂直. |


科目:初中数学 来源: 题型:
 如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )
如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )A、
| ||
B、
| ||
| C、a | ||
| D、2a |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 22、如图,ABCD是正方形,P是对角线BD上一点,过P点作直线EF、GH分别平行于AB、BC,交两组对边于E、F、G、H,则四边形PEDG,四边形PHBF都是正方形,四边形PEAH、四边形PGCF都是矩形,设正方形PEDG的边长是a,正方形PHBF的边长是b. 请动手实践并得出结论:
22、如图,ABCD是正方形,P是对角线BD上一点,过P点作直线EF、GH分别平行于AB、BC,交两组对边于E、F、G、H,则四边形PEDG,四边形PHBF都是正方形,四边形PEAH、四边形PGCF都是矩形,设正方形PEDG的边长是a,正方形PHBF的边长是b. 请动手实践并得出结论:查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
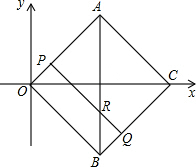 ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
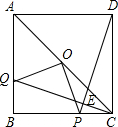 点P,连接OP,OQ;
点P,连接OP,OQ;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com