
 已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:
已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:分析 (1)根据直角三角形斜边上的中线等于斜边的一半可得BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,从而得到BE=DE.
(2)利用等边对等角以及三角形外角的性质得出$\frac{1}{2}$∠DEB=∠DAB,即可得出∠DAB=30°,然后根据四边形内角和即可求得答案.
解答 证明:(1)∵∠ABC=∠ADC=90°,点E是AC边的中点,
∴BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,
∴BE=DE,
∴△BED是等腰三角形;
(2)∵AE=ED,
∴∠DAE=∠EDA,
∵AE=BE,
∴∠EAB=∠EBA,
∵∠DAE+∠EDA=∠DEC,
∠EAB+∠EBA=∠BEC,
∴∠DAB=$\frac{1}{2}$∠DEB,
∵△BED是等边三角形,
∴∠DEB=60°,
∴∠BAD=30°,
∴∠BCD=360°-90°-90°-30°=150°.
故答案为:150.
点评 此题主要考查了等腰三角形的性质和判定以及三角形外角的性质等知识,根据题意得出$\frac{1}{2}$∠DEB=∠DAB是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,∠A=∠D=90°,AD=14,AB=4,CD=6,P是AD上的动点,连接BP,CP,若△PAB∽△CDP,则这样的点P共有( )
如图,在四边形ABCD中,∠A=∠D=90°,AD=14,AB=4,CD=6,P是AD上的动点,连接BP,CP,若△PAB∽△CDP,则这样的点P共有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不可能事件发生的概率是0 | |
| B. | 打开电视机正在播放动画片,是必然事件 | |
| C. | 随机事件发生的概率是 $\frac{1}{2}$ | |
| D. | 对“梦想的声音”节目收视率的调查,宜采用普查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
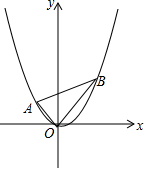 如图,二次函数y=$\frac{2}{3}$x2-$\frac{1}{3}$x,图象过△ABC三个顶点,其中A(-1,m),B(n,n)
如图,二次函数y=$\frac{2}{3}$x2-$\frac{1}{3}$x,图象过△ABC三个顶点,其中A(-1,m),B(n,n)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com