
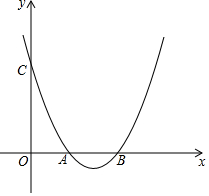
 已知:抛物线y=ax2+bx+c与x轴交于点A(2,0)、B(4,0),且过点C(0,4).
已知:抛物线y=ax2+bx+c与x轴交于点A(2,0)、B(4,0),且过点C(0,4).分析 (1)利用交点式得出y=a(x-1)(x-3),进而得出a的值,再利用配方法求出顶点坐标即可;
(2)根据平移规律:左加右减,上加下减,进而得出答案.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{4a+2b+c=0}&{\;}\\{16a+4b+c=0}&{\;}\\{c=4}&{\;}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-3}\\{c=4}\end{array}\right.$,
∴抛物线解析式为y=$\frac{1}{2}$x2-3x+4;
∵y=$\frac{1}{2}$x2-3x+4=$\frac{1}{2}$(x-3)2-$\frac{1}{2}$,
∴顶点坐标为(3,-$\frac{1}{2}$);
(2)抛物线向左平移3个单位,再向上平移1.5个单位后抛物线的解析式为y=$\frac{1}{2}$x2+1.
点评 此题主要考查了二次函数的平移以及配方法求二次函数解析式顶点坐标以及交点式求二次函数解析式,根据平移规律得出平移后解析式是解题关键.


科目:初中数学 来源: 题型:解答题
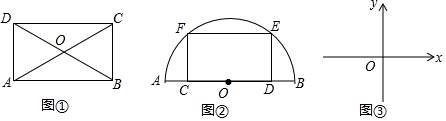
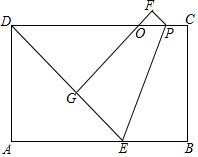 如图,在矩形ABCD中,AD=a,AB=b,E是AB边上一点,且AE=AD,P是线段CD上一点,连结PE,将矩形沿着PE折叠,点B,C分别落在G,F处,FG,CD交于点O.
如图,在矩形ABCD中,AD=a,AB=b,E是AB边上一点,且AE=AD,P是线段CD上一点,连结PE,将矩形沿着PE折叠,点B,C分别落在G,F处,FG,CD交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
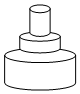 如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )
如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )| A. | 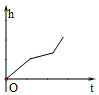 | B. | 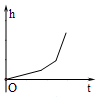 | C. | 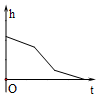 | D. | 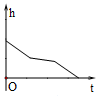 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是8.5 | B. | 中位数是8.5 | C. | 众数是8.5 | D. | 众数是8和9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com