
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:甘肃省平凉市崆峒区2017-2018学年度第一学期期末数学试卷及答案 题型:单选题
如果汽车向南行驶30米记作+30米,那么-50米表示( )
A. 向东行驶50米 B. 向西行驶50米 C. 向南行驶50米 D. 向北行驶50米
D 【解析】【解析】 如果汽车向南行驶30米记作+30米,那么-50米表示向北行驶50米.故选D.查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:单选题
点A为双曲线y=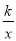 (k≠0)上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为( )
(k≠0)上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为( )
A. 2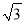 B. ±2
B. ±2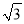 C.
C. 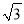 D. ±
D. ±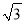
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初一上期中数学试卷数学试卷 题型:解答题
计算: (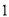 )
)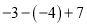 .(
.(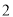 )
)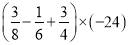 .
.
(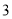 )
)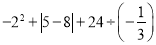 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初一上期中数学试卷数学试卷 题型:单选题
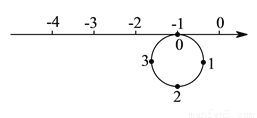
如图,圆的周长为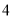 个单位长,在圆的
个单位长,在圆的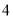 等分点处分别标上
等分点处分别标上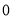 、
、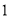 、
、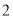 、
、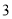 ,先让圆周上表示数字
,先让圆周上表示数字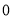 的点与数轴上表示
的点与数轴上表示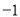 的点重合,再将数轴按逆时针方向环绕在该圆上(如圆周上表示数字
的点重合,再将数轴按逆时针方向环绕在该圆上(如圆周上表示数字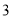 的点与数轴上表示
的点与数轴上表示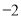 的点重合
的点重合 )依次环绕,则数轴上表示
)依次环绕,则数轴上表示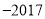 的点与圆周上重合的数字是( ).
的点与圆周上重合的数字是( ).
A. 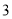 B.
B. 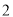 C.
C. 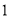 D.
D. 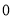
查看答案和解析>>
科目:初中数学 来源:广东省广州市越秀区2016-2017学年八年级下册数学期末考试试卷 题型:解答题
如图,正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP═x,△PBF的面积为S1 ,△PDE的面积为S2 .
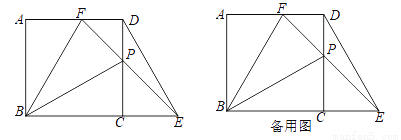
(1)求证:BP⊥DE.
(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围.
(3)分别求当∠PBF=30°和∠PBF=45°时,S1﹣S2的值.
(1)证明见解析;(2)S1﹣S2= x2(0<x<4);(3)①当∠PBF=30°时,S1﹣S2=;②当∠PBF=45°时,S1﹣S2=. 【解析】试题分析:(1)首先延长BP交DE于M.然后依据SAS可证明△BCP≌△DCE,依据全等三角形的性质可得到∠BCP=∠CDE,由∠CBP+∠CPB=90°,∠CPB=∠DPM,即可推出∠CDE+∠DPM=90°; (2)根据题意可得到S1...查看答案和解析>>
科目:初中数学 来源:广东省广州市越秀区2016-2017学年八年级下册数学期末考试试卷 题型:解答题
如图,在△ABC中,AD⊥BC,AB=5,BD=4,CD=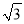 .
.
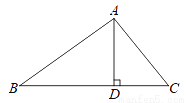
(1)求AD的长.
(2)求△ABC的周长.
(1)3;(2). 【解析】试题分析:(1)在Rt△ABD中,依据勾股定理可求得AD的长; (2)在Rt△ACD中,依据勾股定理可求得AC的长,然后再依据三角形的周长等于三边长度之和求解即可. 试题解析:(1)在Rt△ABD中,AD==3; (2)在Rt△ACD中,AC==2, 则△ABC的周长=AB+AC+BC=5+4++2=9+3.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型:解答题
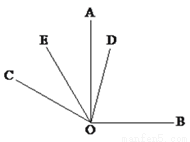
如图,已知同一平面内∠AOB=90°,∠AOC=60°.
(1)填空:∠BOC=__________;
(2)如果OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为_______;
(3)在(2)的条件下,将题目中∠AOC=60°改成∠AOC=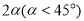 ,其它条件不变,请求出∠DOE的度数.
,其它条件不变,请求出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(北师大版):期中检测题 题型:单选题
已知,直线l经过第二、三、四象限,l的解析式是y=(m﹣2)x+n,则m的取值范围在数轴上表示为( )
A. 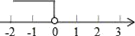 B.
B. 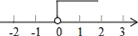
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com