
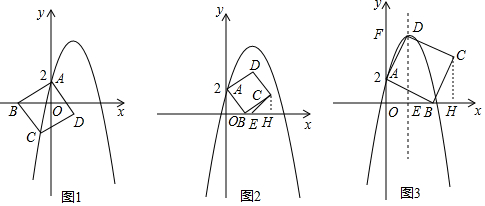
���� ��1���������������ߵĽ���ʽΪy=a��x-2��2+6���ѵ�A��0��2���������a���ɣ�
��2����ͼ1������C��CH��ֱ��x�ᣬHΪ���㣮��AOB�ա�CHB���Ƴ���C������Ϊ��n+2��n�����������߾�����C��n+2��n�����г����̼��ɽ�����⣮
��3������ͼ2����0��n��2ʱ������C��CH��ֱ��x�ᣬHΪ���㣮�ɣ�2����֪��AOB�ա�CHB���Ƴ�BH=AO=2��CH=BO=n���ɵ�E������Ϊ��2��0�����Ƴ�OH=OB+BH=n+2��EH=OH-OE=n+2-2=n���Ƴ�CE=$\sqrt{E{H}^{2}+C{H}^{2}}$=$\sqrt{{n}^{2}+{n}^{2}}$=$\sqrt{2}$n���ɴ˼��ɽ�����⣮
����ͼ3���ֱ����C��D��CH��ֱ��x�ᣬDF��ֱ��y�ᣬH��F��Ϊ���㣮����S��DCE=$\frac{1}{2}$•DE•EH=$\frac{1}{2}$•DC•CE•sin��DCE���������߶μ��ɽ�����⣮
��� �⣺��1���������ߵĶ���Ϊ��2��6�����������ߵĽ���ʽΪy=a��x-2��2+6��
�������߾�����A��0��2����
��4a+6=2��
��a=-1��
�������ߵĽ���ʽΪ��y=-x2+4x+2��
��2����ͼ1������C��CH��ֱ��x�ᣬHΪ���㣮
���ı���ABCD�������Σ�
��AB=BC����ABC=90�㣬
�ߡ�HCB=90��-��HBC=90��=��ABO��
�ڡ�AOB�͡�CHB�У�
$\left\{\begin{array}{l}{��AOB=��BHC}\\{��HCB=��ABO}\\{AB=BC}\end{array}\right.$��
���AOB�ա�CHB��
��BH=AO=2��
��CH=BO=-n����n��0��
��OH=BO-BH=-n-2��
���C��������n+2��n����
�������߾�����C��n+2��n����
��-��n+2��2+4��n+2��+2=n��
��n2+n-6=0��
�ࣨn+3����n-2��=0��
���n=-3��n=2����ȥ����
��n��ֵΪ-3��
��3������ͼ2����0��n��2ʱ������C��CH��ֱ��x�ᣬHΪ���㣮
�ɣ�2����֪��AOB�ա�CHB��
��BH=AO=2��CH=BO=n��
�ߵ�E�ǶԳ�����x��Ľ��㣬
���E��������2��0����
��OH=OB+BH=n+2��
��EH=OH-OE=n+2-2=n��
��CE=$\sqrt{E{H}^{2}+C{H}^{2}}$=$\sqrt{{n}^{2}+{n}^{2}}$=$\sqrt{2}$n��
��CE=$\sqrt{2}$OB��
����ͼ3���ֱ����C��D��CH��ֱ��x�ᣬDF��ֱ��y�ᣬH��F��Ϊ���㣮
���ı���ABCD�������Σ�
��AB=AD=BC=CD����DAB=��ABC=90�㣬
�ߡ�FDA+��FAD=90�㣬��OAB+��FAD=180��-��DAB=180��-90��=90�㣬
���FDA=��OAB��
���FAD�ա�OBA��
��FD=OA=2��AF=OB=n��
�ߵ�D���������ϣ�
���DΪ�����ߵĶ��㣬
��OF=DE=6��n=AF=OF-OA=6-2=4��
ͬ����֤��BH=OA=2��CH=OB=n=4��OH=OB+BH=n+2=4+2=6��EH=OH-OE=6-2=4��
��CD=AD=$\sqrt{A{F}^{2}+F{D}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=$\sqrt{20}$=2$\sqrt{5}$��
CE=$\sqrt{E{H}^{2}+C{H}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$��
��S��DCE=$\frac{1}{2}$•DE•EH=$\frac{1}{2}$��6��4=12��
��S��DCE=$\frac{1}{2}$•DC•CE•sin��DCE=$\frac{1}{2}$��2$\sqrt{5}$��4$\sqrt{2}$��sin��DCE=4$\sqrt{10}$sin��DCE��
��4$\sqrt{10}$sin��DCE=12��
��sin��DCE=$\frac{12}{4\sqrt{10}}$=$\frac{3}{10}$$\sqrt{10}$��
���� ���⿼����κ����ۺ��⡢�����ε����ʡ����ɶ�����ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬ѧ���÷��̵�˼��˼�����⣬�����п�ѹ���⣮


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}x+y=35\\ 18x+24y=750\end{array}\right.$ | B�� | $\left\{\begin{array}{l}x+y=35\\ 24x+18y=750\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}x-y=35\\ 24x-18y=750\end{array}\right.$ | D�� | $\left\{\begin{array}{l}x-y=35\\ 18x-24y=750\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ���O�İ뾶Ϊ3����B=135�㣬��$\widehat{AC}$�ij���������
��ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ���O�İ뾶Ϊ3����B=135�㣬��$\widehat{AC}$�ij���������| A�� | $\frac{��}{2}$ | B�� | �� | C�� | $\frac{3}{2}��$ | D�� | 2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{10}$ | D�� | $\frac{1}{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
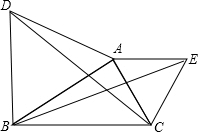 ��ͼ����ABD����AEC���ǵȱ������Σ��߶�BE��DC��������������ϵ��������ת������˵��������ϵ���������ɣ�
��ͼ����ABD����AEC���ǵȱ������Σ��߶�BE��DC��������������ϵ��������ת������˵��������ϵ���������ɣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com