解:(1)∵对称轴为直线x=-

=4,
∴a=-

,
∴抛物线解析式为y=-

x
2+2x;
(2)∵y=-

x
2+2x=-

(x
2-8x+16)+4=-

(x-4)
2+4,
∴顶点坐标为A(4,4),
令y=0,则-

x
2+2x=0,
解得x
1=0,x
2=8,
∴点B的坐标为(8,0),
设直线AB的解析式为y=kx+b,
则

,
解得
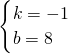
,
所以,直线AB的解析式为y=-x+8,
∵直线l为直线AB平移至经过原点的直线,
∴直线l的解析式为y=-x,
如图,取点A关于直线l的对称点A′,连接A′B交直线l于点P,则△PAB的周长最小,
此时,点A(-4,-4),

点P为线段A′B的中点,
∵

=2,

=-2,
∴点P的坐标为(2,-2);
(3)∵直线AB的解析式为y=-x+8,
∴直线AB与x轴、对称轴的夹角的锐角为45°,
又∵l∥AB,
∴∠POB=45°,
根据勾股定理,AB=

=4

,
PO=

=2

,
①∠BAQ=∠POB=45°时,∵△POB∽△BAQ,
∴

=

,
即
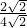
=

,
解得AQ=16,
∴Q的横坐标为16+4=20,纵坐标为4,
∴点Q的坐标为(20,4);
②∠ABQ=∠POB=45°时,∵△POB∽△ABQ,
∴

=

,
即
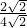
=

,
解得BQ=16,
∴点Q的坐标为(8,16),
综上所述,存在点Q(20,4)或(8,16)使以A,B,Q为顶点的三角形与△POB相似.
分析:(1)利用抛物线对称轴求出a的值,从而得解;
(2)根据抛物线解析式求出点A、B的坐标,然后利用待定系数法求一次函数解析式求出直线AB的解析式,再根据互相平行的直线的解析式的k值相等求出直线l的解析式,再根据轴对称的性质求出点A关于直线l的对称点A′,连接A′B交直线l于点P,然后根据中点公式利用点A′、B的坐标求出点P即可;
(3)根据直线l的解析式可得∠POB=45°,再求出OP、AB的长度,然后分①∠BAQ=∠POB=45°时,②∠ABQ=∠POB=45°时,根据相似三角形对应边成比例列式求出AQ的长度,从而得解.
点评:本题是二次函数综合题型,主要利用了抛物线的对称轴公式,抛物线的对应点坐标,与x轴的交点坐标,利用轴对称确定最短路线问题,相似三角形对应边成比例的性质,(3)根据直线的解析式确定出45°是解题的关键,要注意分情况讨论求解.

 已知如图,对称轴为直线x=4的抛物线y=ax2+2x与x轴相交于点B、O.
已知如图,对称轴为直线x=4的抛物线y=ax2+2x与x轴相交于点B、O. =4,
=4, ,
, x2+2x;
x2+2x; x2+2x=-
x2+2x=- (x2-8x+16)+4=-
(x2-8x+16)+4=- (x-4)2+4,
(x-4)2+4, x2+2x=0,
x2+2x=0, ,
,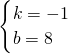 ,
,
 =2,
=2, =-2,
=-2, =4
=4 ,
, =2
=2 ,
, =
= ,
,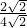 =
= ,
, =
= ,
,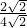 =
= ,
,

 阅读快车系列答案
阅读快车系列答案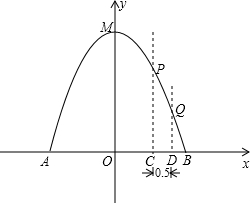 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.