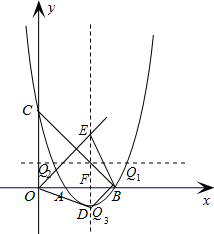
(1)解:分别把A(1,0)、B(3,0)两点坐标代入y=x
2+bx+c得到关于b、c的方程组,
解之得:b=-4,c=3,
∴抛物线的对称轴为:直线x=2;
(2)证明:抛物线的解析式为y=x
2-4x+3,
当x=0时,y=3
∴C点坐标为(0,3),
而y=x
2-4x+3=(x-2)
2-1,
∴抛物线顶点D点坐标为(2,-1).
∴tan∠DOF=

;
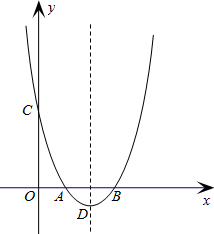
设抛物线的对称轴DE交x轴于点F,
∴F点坐标为(2,0),连接OD,DB,BE.
∵△OBC是等腰直角三角形,OE⊥BC,
∴∠EOB=45°,而OF=2,EF⊥OB,
∴EF=2,
∴E点坐标为(2,2),
∴tan∠ABE=2,
∴∠DAF≠∠ABE,
∴DO与EB不平行.
而△DFB也是等腰直角三角形,
∴∠BOE=∠OBD=45°,
∴OE∥BD,
∴四边形ODBE是梯形.
在Rt△ODF和Rt△EBF中,
OD=
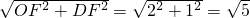
,BE=
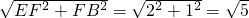
,
∴OD=BE,
∴四边形ODBE是等腰梯形.
(3)解:存在.理由如下:
由题意得:S
四边形ODBE=
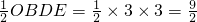
.
设点Q坐标为(x,y).
由题意得:S
三角形OBQ=
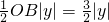
,S
四边形ODBE=
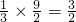
,
∴y=±1.
当y=1时,即x
2-4x+3=1,
∴

,

,
∴Q点坐标为(2+

,1)或(2-

,1)
当y=-1时,即x
2-4x+3=-1,
∴x=2,
∴Q点坐标为(2,-1),即为顶点D.
综上所述,抛物线上存在三点Q
1(2+

,1),Q
2(2-

,1),Q
3(2,-1).
使得S
三角形OBQ=

S
四边形ODBE.
分析:(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数b、c的值,进而可得到抛物线的对称轴方程;
(2)设抛物线的对称轴DE与x轴的交点为F,根据抛物线的对称轴方程即可求得F点的坐标;根据抛物线的解析式可求出C、D的坐标,即可证得△OBC、△BDF都是等腰直角三角形,那么∠DBF=∠CBA=∠EOB=45°,由此可证得OE∥BD,然后再根据O、D、B、E四点坐标求出OD、BE的长,即可证得所求的结论;
(3)首先求出四边形ODBE的面积,进而可得到△OBQ的面积,由于OB的长为定值,根据△OBQ的面积即可确定Q点纵坐标的绝对值,将其代入抛物线的解析式中即可求得Q点的坐标.
点评:此题主要考查了二次函数解析式的确定、等腰梯形的判定以及图形面积的求法等知识的综合应用能力.

 点为D.
点为D. ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由. (1)解:分别把A(1,0)、B(3,0)两点坐标代入y=x2+bx+c得到关于b、c的方程组,
(1)解:分别把A(1,0)、B(3,0)两点坐标代入y=x2+bx+c得到关于b、c的方程组, ;
;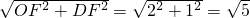 ,BE=
,BE=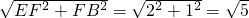 ,
,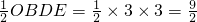 .
.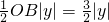 ,S四边形ODBE=
,S四边形ODBE=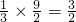 ,
, ,
, ,
, ,1)或(2-
,1)或(2- ,1)
,1) ,1),Q2(2-
,1),Q2(2- ,1),Q3(2,-1).
,1),Q3(2,-1). S四边形ODBE.
S四边形ODBE.

 阅读快车系列答案
阅读快车系列答案 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.