
���г��ȵ����߶Σ�����ɵ��������ε��ǣ� ��
A. 1��1��2 B. 2��2��5 C. 3��3��5 D. 3��4��5
C ���������������� A����1+1=2�������������Σ��ʴ�ѡ����� B����2+2��5�������������Σ��ʴ�ѡ����� C����3+3��5��3=3������ɵ��������Σ���ѡ����ȷ�� D����3��4��5û����ȵıߣ����ǵ��������Σ��ʴ�ѡ����� ��ѡ��C�� ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�γ���2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ������
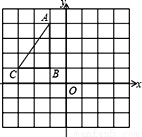
��ͼ����ֱ������ϵ�У�Rt��ABC����������ڱ߳�Ϊ1���������������ϣ�
��1��������ABC����y��ԳƵġ�A��B��C�䣻
��2������y�����е� D��0,2�����������������еĸ���ϣ���A��C��D��EΪ������ı���Ϊƽ���ı��Σ�����ͼ�б����E����ֱ��д����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����а�����2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ������֪�ġ�ABC�У������²�����ͼ��
�ٷֱ���B��CΪԲ�ģ��Դ���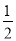 BC�ij�Ϊ�뾶�����������ཻ������M��N��
BC�ij�Ϊ�뾶�����������ཻ������M��N��
����ֱ��MN��AB�ڵ�D������CD��
��CD=AC����A=50�㣬���ACB�Ķ���Ϊ��������
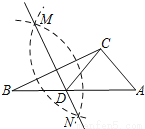
A. 90�� B. 95�� C. 100�� D. 105��
D ����������������ͼ����֪��MNΪ�߶�BC�Ĵ�ֱƽ���ߣ� ��CD=BD�� ���B=��BCD�� ��CD=AC�� ���ADC=��A=50�㣬 �ߡ�ADC=��B+��BCD�� ��2��B=50�㣬���B=25�㣬 �ߡ�A+��B+��ACB=180�㣬 ���ACB=180��-��A-��B=105�㣬 ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����в�2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
��A��x��3������y��ĶԳƵ���B����2��y������x=____ ,y=______ ,��A����x��ĶԳƵ��������___________ ��
2�� 3 (2,-3) �������������������A��x��3������y��ĶԳƵ���B��-2��y���� ��x=2��y=3�� ��A��2��3���� ���A����x��ĶԳƵ�������ǣ�2��-3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����в�2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ���ѡ��
�������������εĸߣ�����˵������ȷ���ǣ� ��
A. ����������������� B. ֱ��������ֻ��һ����
C. ���������ζ��������� D. �۽����������������������ε��ⲿ
B ��������������������������εĸߵĸ��ͨ���������ߣ����֣�����һ�������ζ��������ߣ�������������ε������߶��������ε��ڲ���ֱ���������������������ε�����ֱ�DZߣ�һ�����ڲ����۽����������������������ε��ⲿ��һ�����ڲ����ݴ˿�֪�� A������������������ߣ�˵����ȷ���ʱ�ѡ��������⣻ B��ֱ���������������ߣ�˵�����ʱ�ѡ��������⣻ C�����������ζ��������ߣ�...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ������
Ϊ��ǿѧ�����������ijУ��չ��������μ䡱���ѧУ������ѧ���п���A������B��������Զ��C��������D���ܲ���E���������ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ��ʾ������ͳ��ͼ������ͼ�е���Ϣ����������⣺
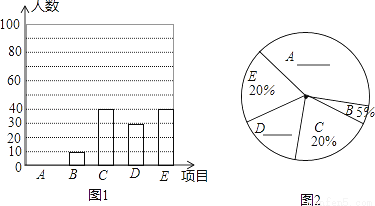
��1������������У���������_______��ѧ����
��2���뽫����ͳ��ͼ����������
��3������У��1200����Уѧ���������ϲ�������ѧ����Լ�ж����ˣ�
*1��200����2����ͼ����������3��240�ˣ� ����������������� ��1����ͼ1�ɵ�ϲ����B���˶�������10�ˣ���ͼ2�ɵ�ϲ����B���˶�����ռ������5%����10��5%�������������Ϊ200�ˣ� ��2������ͼ1��֪ϲ��B��C��D��E�����˶��������ֱ�Ϊ10��40��30��40�ˣ��ɴ˿ɵ�ϲ��A���˶�������Ϊ��200-10-40-30-40=80���ɴ���ͼ1�в�����ʾA�����μ��ɣ���...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ������
��ͼ����O��ֱ��AB����CD���е�E������C=25�㣬���D=________��
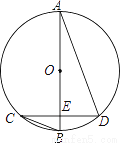
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ������
��ͼ��ABΪ��ԲO��ֱ����CΪBA�ӳ�����һ�㣬CD�а�ԲO�ڵ�D������OD����BE��CD�ڵ�E������ԲO�ڵ�F����֪CE=12��BE=9,
(1)��֤����COD�ס�CBE��
(2)���ԲO�İ뾶�ij�
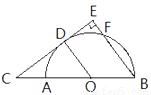
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶����ĩģ����ѧ�Ծ������𰸣� ���ͣ���ѡ��
�������ڳ߹���ͼ���ǣ�������
A. �ÿ̶ȳߺ�Բ������ABC B. ����������һ��300�Ľ�
C. ��Բ�滭�뾶2cm��Բ D. ��һ���߶ε�����֪�߶�
D ����������һ���߶ε�����֪�߶����ڳ߹���ͼ.��ѡD.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com