
(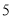 分)如图,在
分)如图,在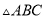 中,
中, 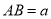 ,
, 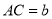 .请用尺规作一条直线
.请用尺规作一条直线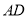 ,使其将
,使其将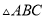 面积分为
面积分为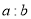 两部分.(保留作图痕迹,不写作法)
两部分.(保留作图痕迹,不写作法)
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:填空题
已知BD=4,延长BD到A,使BA=6,点C是线段AB的中点,则CD=__.
1 【解析】∵C为AB的中点,BA=6, ∴BC=AB==3, ∵BD=4, ∴CD=BD-BC=4-3=1, 故答案为:1.查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:解答题
如图,一次函数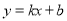 与反比例函数
与反比例函数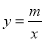 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式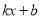 <
<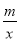 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:填空题
国家对药品实施价格调整,某药品经过两次降价后,每盒的价格由原来的60元降至48.6元,那么平均每次降价的百分率是________________.
10% 【解析】试题解析:设平均每次降价的百分率为x,某种药品经过两次降价后,每盒的价格由原来的60元降至48.6元,可列方程:60(1-x)2=48.6. 故答案为:60(1-x)2=48.6.查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(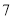 分)周末,小英与她的父亲、母亲计划从西安外出旅游,初步选择了位于西安东线的景点
分)周末,小英与她的父亲、母亲计划从西安外出旅游,初步选择了位于西安东线的景点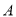 :兵马俑,
:兵马俑, 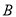 :华山,以及位于西线的景点
:华山,以及位于西线的景点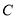 :太白山,
:太白山, 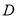 :法门寺,
:法门寺, 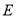 :杨凌现代农业示范园.由于时间仓促,他们只能去其中的两个景点,并且希望两个景点能位于一条线路上.到底去哪两个景点,三人意见不统一.在这种情况下,小英父亲建议,用小英学过的摸卡片游戏来决定.规则如下:在五个背面完全相同的卡片上写上五个景点的代号,然后洗匀,背面朝上放在桌面上,让小英随机摸出一张,不放回,然后让小英母亲再随机摸出一张.照上面的规则,请你解答下列问题:
:杨凌现代农业示范园.由于时间仓促,他们只能去其中的两个景点,并且希望两个景点能位于一条线路上.到底去哪两个景点,三人意见不统一.在这种情况下,小英父亲建议,用小英学过的摸卡片游戏来决定.规则如下:在五个背面完全相同的卡片上写上五个景点的代号,然后洗匀,背面朝上放在桌面上,让小英随机摸出一张,不放回,然后让小英母亲再随机摸出一张.照上面的规则,请你解答下列问题:
(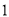 )己知小英的理想旅游景点是兵马俑,求小英摸出写有
)己知小英的理想旅游景点是兵马俑,求小英摸出写有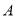 的卡片的概率.
的卡片的概率.
(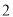 )求小英和母亲摸出的景点位于一条线上(东线或西线)的概率.
)求小英和母亲摸出的景点位于一条线上(东线或西线)的概率.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:填空题
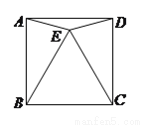
在正方形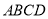 内,以
内,以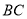 为边作等边
为边作等边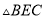 ,连接
,连接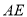 、
、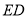 ,则
,则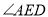 的大小为__________.
的大小为__________.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:单选题
某商品原价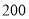 元,连续两次降价后售价为
元,连续两次降价后售价为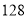 元,若设两次降价的平均降价率为
元,若设两次降价的平均降价率为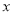 ,则下列所列方程,正确的是( ).
,则下列所列方程,正确的是( ).
A. 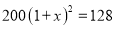 B.
B. 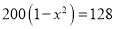 C.
C. 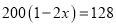 D.
D. 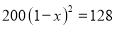
查看答案和解析>>
科目:初中数学 来源:人教版九年级年级数学下册第二十九章 达标检测卷 题型:单选题
图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN的度数为( )
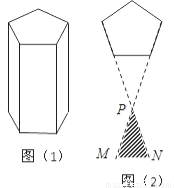
A.30° B.36° C.45° D.72°
B 【解析】 根据正五边形的内角为108°,观察图形,利用三角形内角和为180°,和对顶角相等,可求出∠MPN的度数. 【解析】 由题意我们可以得出,正五棱柱的俯视图中,正五边形的内角为=108°, 那么∠MPN=180°﹣(180°﹣108°)×2=36°. 故选B.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:解答题
如果∠A与∠B的两条边分别平行,其中∠A=(x+30)°;∠B =(3x-10)°,那么∠A的度数为________
50°或70° 【解析】(1)如图(1) 由题意知:AM//BE,AN//BF, ∴∠A=∠1=(x+30)°,∠2+∠B=180° 又∠1=∠2,∴∠2=∠A=(x+30)°, 又∠B=(3x-10)°, ∴ ,解得x=40, ∴∠A=(40+30)°=70°. (2)如图(2,), 由题意知:AM//BE,AN//BF, ∴∠1=∠A...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com