
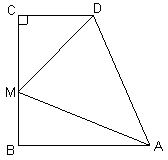
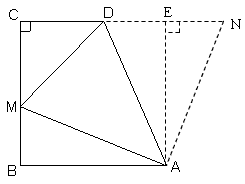
| 解:(1)证明:作AE⊥CD交延长线于点E, ∵∠DMC=45°,∠C=90°, ∴CM=CD, 又∵∠B=∠C=∠E=90°,AB=BC, ∴四边形ABCE为正方形, ∴BC=CE, ∴BM=DE, 在Rt△ABM和Rt△AED中, ∴△ABM≌△AED, ∴AD=AM。 (2)把Rt△ABM绕点A顺时针旋转90°,使AB与AE重合, 得Rt△AEN, ∵∠DAM=45°, ∴∠BAM+∠DAE=45°, 由旋转知∠1=∠3, ∴∠2+∠3=45°, 即∠DAM=∠DAN, 由旋转知AM=AN, ∴△ADM≌△ADN, ∴DM=DN, 设BM=x, ∵AB=BC=CE=7, ∴CM=7-x, 又∵CD=4, ∴DE=3,BM=EN=x, ∴MD=DN=3+x, 在Rt△CDM中,(7-x)2+42=(3+x)2,x= 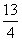 , ,∴BM的值为 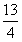 。 。 |
 |


科目:初中数学 来源: 题型:
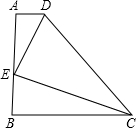 下结论:
下结论:| A、2个 | B、3个 | C、4个 | D、5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
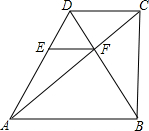 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com