Question

已知函数y=-x+4的图象与x轴、y轴分别交于点A、D，与双曲线交于点B、C，若AB+CD=BC，则k的值为

1. A.
   2
2. B.
   3
3. C.
   4
4. D.
   8

Answer 1

B
分析：根据题意画出相应的图形，过C作CF⊥x轴，交x轴于点F，过B作BG⊥y轴，交y轴于点G，两垂线交于E点，如图所示，对于一次函数分别求出A与D的坐标，得到三角形OAD为等腰直角三角形，利用勾股定理求出AD的长，由AB+CD=BC，得到BC的长为AD的一半，求出BC的长，联立两函数解析式，消去y得到关于x的一元一次方程，设方程两根分别为x₁，x₂，即C（x₁，y₁），B（x₂，y₂），则有x₁+x₂=4，x₁x₂=k，表示出CE与BE，在直角三角形BCE中，利用勾股定理列出关系式，将各自的值代入变形后，将两根之和与两根之积代入列出关于k的方程，求出方程的解即可的k的值．
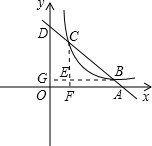
解答：解：过C作CF⊥x轴，交x轴于点F，过B作BG⊥y轴，交y轴于点G，两垂线交于E点，如图所示，
对于一次函数y=-x+4，
令y=0，求出x=4；令x=0，求出y=4，
∴A（4，0），D（0，4），
∴△AOD为等腰直角三角形，即AD=4，
联立两函数解析式得：，
消去y得到：x²-4x+k=0，
∵△=16-4k＞0，即k＜4，
∴设方程两根分别为x₁，x₂，即C（x₁，y₁），B（x₂，y₂），则有x₁+x₂=4，x₁x₂=k，
∵AB+CD=BC，
∴BC=AD=2，
∵CE=y₂-y₁=-x₁+4-（-x₂+4）=x₂-x₁，BE=x₁-x₂，
∴根据勾股定理得：BC²=CE²+BE²，即（x₁-x₂）²+（x₂-x₁）²=2（x₁-x₂）²=8，即（x₁-x₂）²=4，
∴（x₁+x₂）²-4x₁x₂=4，即16-4k=4，
解得：k=3．
故选B．
点评：此题考查了反比例函数与一次函数的交点问题，涉及的知识有：根与系数的关系，完全平方公式的运用，一次函数与坐标轴的交点，坐标与图形性质，是一道综合性较强的试题．