
 BC,B、C两点的坐标分别为B(1,0)、
BC,B、C两点的坐标分别为B(1,0)、 ,且当x=-10和x=8时函数的值y相等.
,且当x=-10和x=8时函数的值y相等.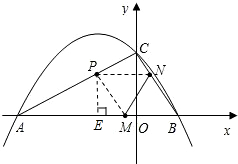 解:(1)∵当x=-10和x=8时函数的值y相等,
解:(1)∵当x=-10和x=8时函数的值y相等, ,
,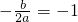 ,
,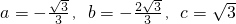 ;
;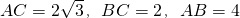 .
.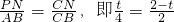 ,∴
,∴ .
. ,
, sin60°=
sin60°= ,
, -1=
-1= ,OE=1.
,OE=1. );
); (x+1)2+k.
(x+1)2+k.
 )或(-1,-
)或(-1,- )
) (x+1)2+
(x+1)2+ 或y=-
或y=- (x+1)2-
(x+1)2-

 )或(-1,-
)或(-1,- )
) (x+1)2+
(x+1)2+ 或y=-
或y=- (x+1)2-
(x+1)2-
 (x+1)2+
(x+1)2+ 或y=-
或y=- (x+1)2-
(x+1)2- 或y=-
或y=- (x+1)2+
(x+1)2+ 或y=-
或y=- (x+1)2-
(x+1)2- .
. ,得∠OBC=60°,若△BMN沿MN翻折,B点恰好落在AC边上的P处,那么四边形MBNP为菱形,此时NP=BM=t,易得△CPN∽△CAB,根据相似三角形得到的比例线段,即可求得t的值,由此可得PM的长,过P作PE⊥AB于E,由于∠PMA=60°,通过解直角三角形,可得到ME、PE的长,进而求得点P的坐标;
,得∠OBC=60°,若△BMN沿MN翻折,B点恰好落在AC边上的P处,那么四边形MBNP为菱形,此时NP=BM=t,易得△CPN∽△CAB,根据相似三角形得到的比例线段,即可求得t的值,由此可得PM的长,过P作PE⊥AB于E,由于∠PMA=60°,通过解直角三角形,可得到ME、PE的长,进而求得点P的坐标; ,即D点纵坐标的绝对值为
,即D点纵坐标的绝对值为 ,可据此求出平移后的抛物线解析式;
,可据此求出平移后的抛物线解析式; ,即D点纵坐标的绝对值为
,即D点纵坐标的绝对值为 ,就可求得平移后的抛物线解析式.
,就可求得平移后的抛物线解析式.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 9 |
| 8 |
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
 O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:
 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,查看答案和解析>>
科目:初中数学 来源: 题型:
 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com