
下列各式中,满足完全平方公式进行因式分解的是( )
A. 4x2-12xy+9y2 B. 2x2+4x+1 C. 2 x2+4xy+y2 D. x2-y2+2xy
A 【解析】试题解析:A、4x2-12xy+9y2=(2x-3y)2,能用完全平方公式进行因式分解,故此选项正确; B、2x2+4x+1,不能用完全平方公式进行因式分解,故此选项错误; C、2x2+4xy+y2,不能用完全平方公式进行因式分解,故此选项错误; D、x2-y2+2xy,不能用完全平方公式进行因式分解,故此选项错误. 故选A.科目:初中数学 来源:四川省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列四个命题中,真命题有( )
①内错角一定相等;②如果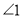 和
和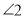 是对顶角,那么
是对顶角,那么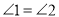 ;③三角形的一个外角大于任何一个与它不相邻的内角;④若
;③三角形的一个外角大于任何一个与它不相邻的内角;④若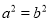 ,则
,则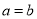 .
.
A. 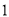 个 B.
个 B. 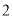 个 C.
个 C. 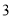 个 D.
个 D. 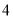 个
个
查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级上学期期末考试数学试卷 题型:填空题
点P(1,-1)关于原点对称的点的坐标是_________.
(-1,1) 【解析】点P(1,-1)关于原点对称的点的坐标是(-1, 1). 故答案为(-1, 1).查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型:解答题
如图,在△ABC中,AC=5,BC=12,AB=13,D是BC的中点,求AD的长和△ABD的面积.
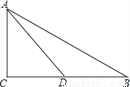
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型:填空题
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线上一个动点,若PA=3,则PQ的最小值为______
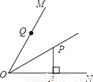
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型:单选题
下列二次根式中可以和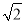 相加合并的是( )
相加合并的是( )
A. 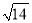 B.
B. 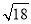 C.
C. 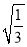 D.
D. 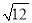
查看答案和解析>>
科目:初中数学 来源:江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:① ;②
;② .
.
(2)若 ,
,
① 如图2,点E在正方形内,连接EC,若 ,
,  ,求
,求 的长;
的长;
② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.



查看答案和解析>>
科目:初中数学 来源:江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
“生态兴化,如诗如画”.我市正全力打造成国家全域旅游示范区,为调查我市市民对兴化全域旅游的情况了解,宜采用_________(填“普查”或“抽样调查”)的方式.
抽样调查 【解析】【解析】 采用抽样调查的方式.故答案为:抽样调查.查看答案和解析>>
科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:填空题
方程2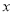 ﹣5=7的解与关于
﹣5=7的解与关于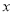 的方程
的方程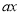 +3=9的解相同,那么
+3=9的解相同,那么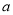 的值为___________.
的值为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com