已知A(-2,3),B(3,1),P点在x轴上,若PA+PB长度最小,则最小值为________;若PA-PB长度最大,则最大值为________.


分析:(1)找到B点关于x轴的对称点B′,连接AB′交x轴于点P,即可得到要求的P点,再根据一次函数的性质,找到各点的坐标,即可得出答案.
(2)根据三角形的性质,两边之差小于第三边,连接AB交x轴于点P,即可得到要求的P点,则可知AB的长度即为所求.
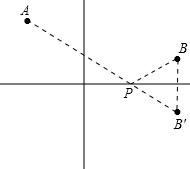
解答:(1)求最小值:如图所示:
,
作B点关于x轴的对称点B',连接AB′,交x轴于点P,
∵B和B′对称,
∴PB=PB′,
∴AP+BP=PA+B′P,
根据两点之间线段最短可知P点为所求.
∵已知A(-2,3),B(3,1),
∴B′坐标为(3,-1),
则可求得最短距离为AB′的长度,AB′=
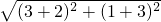
=

,
∴PA+PB长度最小,则最小值为

.
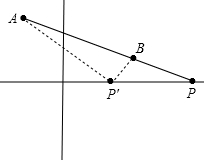
(2)求最大值:如图所示:
,
连接AB并延长,交x轴于点P,
任取一点P',连接AP'、BP',
在△ABP'中,根据三角形的性质,两边之差小于第三边,
即AP'-BP'<AB,
∴可知AB为所求的最大值,
∵已知A(-2,3),B(3,1),
AB=
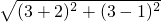
=

,
∴若PA-PB长度最大,则最大值为

.
点评:本题属于综合性的试题,包含了一次函数的应用、对称图形的性质、三角形的性质以及最大值最小值的求法.解决这类题目要求对于所学的各种知识点要能够融会贯通,达到“信手拈来”的地步.



 ,
,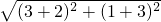 =
= ,
, .
. ,
,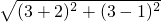 =
= ,
, .
.

 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.