练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

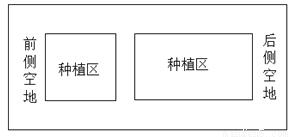
    某村计划建造如图所示的矩形蔬菜温室，要求长宽的比为3：1，在温室内，沿前后两侧的内墙各留2.5m宽的空地放置工具，其他两侧内墙各留1m宽的通道．中间区域再留1m宽的通道，通道与前后墙平行，剩余空地（阴影部分）为种植区，当种植区面积是300m2，求矩形温室的长与宽是多少？

    长为36m、宽为12m． 【解析】试题分析：首先设长为3xm，则宽为xm，然后根据题意列出关于x的一元二次方程，从而求出x的值，从而得出长和宽． 试题解析：【解析】 设长为3xm，则宽为xm，根据题意列方程得： （3x-6）（x-2）=300． 解之得： x1=-8（舍去），x2=12m∴3x=36m 答：矩形温室的长为36m、宽为12m，种植区面积为300m...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型：解答题

    阅读下面解答过程，并填空或填理由．

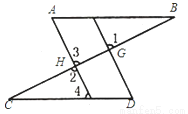
    已知如下图，点E、F分别是AB和CD上的点，DE、AF分别交BC于点G、H，∠A=∠D，∠1=∠2．

    试说明：∠B=∠C．

    【解析】
    ∵∠1=∠2（已知）

    ∠2=∠3（___________）

    ∴∠3=∠1（等量代换）

    ∴AF∥DE（___________）

    ∴∠4=∠D（___________）

    又∵∠A=∠D（已知）

    ∴∠A=∠4（等量代换）

    ∴AB∥CD（___________）

    ∴∠B=∠C（___________）．

    对顶角相等 同位角相等，两直线平行 两直线平行，同位角相等 内错角相等，两直线平行 两直线平行，内错角相等 【解析】试题分析：根据对顶角的性质填第一个空，根据平行线的判定填第二和第四个空，根据平行线的性质填第三和第五个空． 试题解析：∵∠1=∠2（已知） ∠2=∠3（对顶角相等） ∴∠3=∠1（等量代换） ∴AF∥DE（同位角相等，两直线平行） ∴∠4=∠D（两...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：解答题

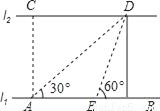
    如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB=60°，求C、D两点间的距离．

    C、D两点间的距离为30m． 【解析】直接利用等腰三角形的判定与性质得出DE=AE=20，进而求出EF的长，再得出四边形ACDF为矩形，则CD=AF=AE+EF求出答案． 【解析】 过点D作l1的垂线，垂足为F， ∵∠DEB=60°，∠DAB=30°， ∴∠ADE=∠DEB﹣∠DAB=30°， ∴△ADE为等腰三角形， ∴DE=AE=20， 在Rt△DE...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    连续四次抛掷一枚硬币都是正面朝上，则“第五次抛掷正面朝上”是（　　）

    A. 必然事件 B. 不可能事件

    C. 随机事件 D. 概率为1的事件

    C 【解析】硬币落地时，只有正面朝上和反面朝上两种情况，所以第五次抛掷正面朝上是随机事件， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    如图所示的几何体是由5个大小相同的小正方体紧密摆放而成的，其三视图中面积最大的是（　　）

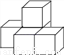
    A. 主视图 B. 左视图 C. 俯视图 D. 主视图和俯视图

    D 【解析】如图，该几何体主视图是由4个小正方形组成， 左视图是由3个小正方形组成， 俯视图是由4个小正方形组成，故三种视图面积最小的是左视图． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：填空题

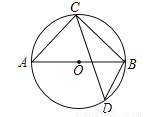
    如图AB是⊙O的直径，C，D是⊙O上的两点，若∠BCD=28°，则∠ABD=___________．

    62 【解析】试题分析：连接AD，根据AB是直径，可知∠ADB=90°，然后根据同弧所对的圆周角可得∠BAD=∠DCB=28°，然后根据直角三角形的两锐角互补可得∠ABD=62°. 故答案为：62.

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：单选题

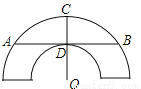
    如图是一个古代车轮的碎片，小明为求其外圆半径，连接外圆上的两点A，B，并使AB与车轮内圆相切于点D，半径OC⊥AB交外圆于点C，测得CD=10cm，AB=60cm，则这个车轮的外圆半径是（　　）

    A. 10cm B. 30cm C. 60cm D. 50cm

    D 【解析】试题分析：连接OB，根据垂径定理可得：BD=30cm，△BOD为直角三角形，设OB=rcm，则OD=(r-10)cm，根据Rt△BOD的勾股定理可得： ，解得：r=50cm，故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省中考数学模拟试卷 题型：单选题

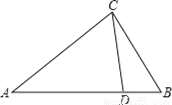
    如图，△ACD和△ABC相似需具备的条件是（　　）

    A. 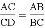B. 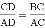C. AC2=AD•AB D. CD2=AD•BD

    C 【解析】试题分析：本题主要考查的就是三角形相似的判定，本题根据有一个角相等，且对应角的两边对应成比例，则两个三角形相似可以得出答案.根据题意可得∠A为公共角，则要使三角形相似则必须满足=. 点晴：本题主要考查的就是三角形相似的判定定理，在有一个角相等的情况下，必须是角的两边对应成比例，如果不是角的两边对应成比例，则这两个三角形不相似；相似还可以利用有两个角对应相等的两个三角形全等....

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上期末复习检测数学试卷 题型：解答题

    阅读材料

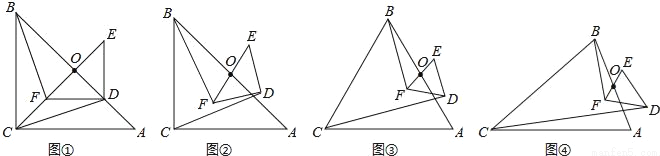
    如图①，△ABC与△DEF都是等腰直角三角形，∠ACB=∠EDF=90°，且点D在AB边上，AB、EF的中点均为O，连结BF、CD、CO，显然点C、F、O在同一条直线上，可以证明△BOF≌△COD，则BF=CD．

    解决问题

    （1）将图①中的Rt△DEF绕点O旋转得到图②，猜想此时线段BF与CD的数量关系，并证明你的结论；

    （2）如图③，若△ABC与△DEF都是等边三角形，AB、EF的中点均为O，上述（1）中的结论仍然成立吗？如果成立，请说明理由；如不成立，请求出BF与CD之间的数量关系；

    （3）如图④，若△ABC与△DEF都是等腰三角形，AB、EF的中点均为0，且顶角∠ACB=∠EDF=α，请直接写出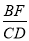的值（用含α的式子表示出来）

    （1）猜想：BF=CD．理由见解析； （2）（1）中的结论不成立，理由见解析； （3）=tan． 【解析】试题分析：（1）如答图②所示，连接OC、OD，证明△BOF≌△COD； （2）如答图③所示，连接OC、OD，证明△BOF∽△COD，相似比为； （3）如答图④所示，连接OC、OD，证明△BOF∽△COD，相似比为tan． 试题解析：（1）猜想：BF=CD．理...

    查看答案和解析>>

    同步练习册答案