
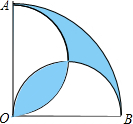
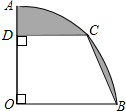
 如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是
如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是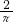
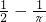
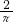
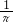
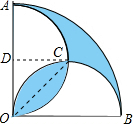 解:设OA的中点是D,则∠CDO=90°,半径为r
解:设OA的中点是D,则∠CDO=90°,半径为r πr2
πr2 π(
π( )2=
)2= πr2
πr2 ×
× ×
× =
= r2
r2 S半圆OAC-S△ODC=
S半圆OAC-S△ODC= πr2-
πr2- r2
r2 πr2-
πr2- r2
r2 πr2-2×
πr2-2× πr2+2(
πr2+2( πr2-
πr2- r2)=
r2)= πr2-
πr2- r2
r2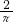 .
.

科目:初中数学 来源: 题型:
 |
| AB |
 为G.
为G. |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
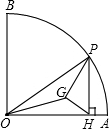
 如图,在半径为2,圆心角等于90°的扇形AOB内部作一个直角梯形OBCD,使点C在
如图,在半径为2,圆心角等于90°的扇形AOB内部作一个直角梯形OBCD,使点C在 |
| AB |
 |
| AB |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2004年浙江省绍兴市嵊州市初三数学竞赛试卷(解析版) 题型:解答题
 上,有一个动点P,PH⊥OA,垂足为H,△OPH的重心为G.
上,有一个动点P,PH⊥OA,垂足为H,△OPH的重心为G. 上运动时,线段GO、GP、GH中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度;
上运动时,线段GO、GP、GH中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度;
查看答案和解析>>
科目:初中数学 来源:2005年浙江省温州市永嘉县桥下镇中学初三数学竞赛试卷(解析版) 题型:解答题
 上,有一个动点P,PH⊥OA,垂足为H,△OPH的重心为G.
上,有一个动点P,PH⊥OA,垂足为H,△OPH的重心为G. 上运动时,线段GO、GP、GH中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度;
上运动时,线段GO、GP、GH中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com