
科目:初中数学 来源:北京市石景山区2018届九年级中考二模数学试卷 题型:解答题
在平面直角坐标系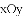
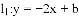 与
与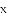
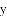
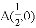 ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为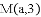 .
.
(1)求反比例函数的表达式;
(2)设直线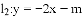 与
与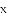
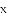
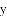
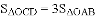 ,直接写出
,直接写出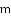
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳市双清区2018届九年级中考数学模拟试卷 题型:解答题
如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为 ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得




(2)连接CD,根据直径所对的圆周角是直角,即可得





试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),

∴ED⊥OD,
∴ED是
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,

∵OE∥AB,
∴△COE∽△CAB,
 ∴AB=5,
∴AB=5,
∵AC是直径,




∵EF∥AB,



∴S△ADF=S梯形ABEF?S梯形DBEF

∴△ADF的面积为

【题型】解答题
【结束】
23
一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

查看答案和解析>>
科目:初中数学 来源:湖南省邵阳市双清区2018届九年级中考数学模拟试卷 题型:单选题
一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在这个位置小正方体的个数.从左面看到的这个几何体的形状图的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省淮安市淮安区2016-2017学年八年级(下)第一次月考数学试卷 题型:填空题
已知,如图,在□ABCD中,AB=5cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=_____cm.

查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级下学期第二次月考数学试卷 题型:解答题
阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如: ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设 (其中
(其中
 .
.
∴ .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当
 ,用含m、n的式子分别表示
,用含m、n的式子分别表示


(2)利用所探索的结论,找一组正整数
 =( +
=( +  )2;
)2;
(3)若 ,且
,且

【答案】(1) ;
;

【解析】分析:(1)由a+b =(m+n
=(m+n )2,展开比较系数可得答案;
)2,展开比较系数可得答案;
(2)取m=1,n=1,可得a和b的值,可得答案;
(3)由题意得m和n的方程,解方程可得m和n,可得a值.
详【解析】
(1)∵a+b =(m+n
=(m+n )2,
)2,
∴a+b =m2+3n2+2mn
=m2+3n2+2mn ,
,
∴a=m2+3n2,b=2mn.
故答案为:m2+3n2,2mn.
(2)设m=1,n=1,
∴a=m2+3n2=4,b=2mn=2.
故答案为4、2、1、1.
(3)由题意,得:
a=m2+3n2,b=2mn
∵4=2mn,且m、n为正整数,
∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.
点睛:本题主要考查二次根式的混合运算,完全平方公式,解题的关键在于熟练运算完全平方公式和二次根式的运算法则.
【题型】解答题
【结束】
28
如图1,已知点A(a,0),B(0,b),且a、b满足 ,
,
□ABCD的边AD与y轴交于点E,且E为AD中点,双曲线 经过C、D两点.
经过C、D两点.
(1)若点D点纵坐标为t,则C点纵坐标为 (含t的代数式表示),k的值为 ;
(2)点P在双曲线 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,连接FN,当T在AF上运动时,试判断∠ATH 与∠AFN 之间的数量关系,并说明理由。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com