练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如下图所示，已知OA⊥OB，OC⊥OD，∠BOC∶∠AOD＝3∶5，求∠BOC的度数．

    答案：67.5°
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：新教材完全解读　七年级数学下册　人教版 人教版 题型：044

    如下图所示，已知OA⊥OD于点O，OC⊥OB于点O，∠AOB＝130°，求∠COD和∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　下册(配北师大版新课标) 北师大版新课标 题型：044

    如下图所示，已知A为∠POQ的边OQ上一点，以A为顶点的∠MAN的两边分别交射线OP于M，N两点，且∠MAN＝∠POQ＝α(α为锐角)．当∠MAN以点A为旋转中心，AM边从与AO重合的位置开始，按逆时针方向旋转(∠MAN保持不变)时，M，N两点在射线OP上同时以不同的速度向右平移．设OM＝x，ON＝y(y＞x≥0)，△AOM的面积为S，且cosα，OA是方程2z2－5z＋2＝0的两个根．

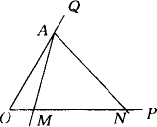
    (1)当∠MAN旋转30°(即∠OAM＝30°)时，求点N移动的距离；

    (2)求证AN2＝ON·MN；

    (3)试求y与x之间的函数关系式及自变量x的取值范围；

    (4)试写出S随x变化的函数关系式，并确定S的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　下册(配北师大版新课标) 北师大版新课标 题型：022

    如下图所示，已知OA，OB是圆的两条半径，∠OAB＝45°，OA＝5，则AB＝________．

    查看答案和解析>>

    科目：初中数学 来源：专项题 题型：解答题

    请阅读下题及其证明过程，并回答所提出的问题，如下图所示，已知P为⊙O外一点，PA、PB为⊙O的切线，A和B是切点，BC为直径，求证：AC∥OP。
    证明：连AB，交OP于点D，连OA
    ∵PA、PB切⊙O于AB
    ∴OA⊥PA，OB⊥PB
    又∵OA=OB，OP=OP
    ∴△OAP≌△OBP
    ∴∠3=90°
    _______
    ∴∠4=90°
    ∴∠3=∠4
    ∴AC∥OP。
    （1）在横线上补上应填的条件；
    （2）上述证明过程中用到的定理具体内容是（只要求写出两个）。

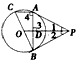
    查看答案和解析>>

    同步练习册答案