
��һ�������ĺ����װ���ĸ��ֱ��������1��2��3��4��С�����ǵ���״����С���ʵص���ȫ��ͬ��С���ȴӺ��������ȡ��һ��С��������Ϊx���Żغ���ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy��
��1�����б�����ʾ����x��y�������п��ܳ��ֵĽ����
��2����С����С����ȡһ��С����ȷ���ĵ㣨x��y�����ڷ���������y=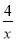 ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�
��3����С����С����ȡһ��С����ȷ������x��y����y��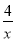 �ĸ��ʣ�
�ĸ��ʣ�
 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�������п���ѧģ���Ծ� ���ͣ������
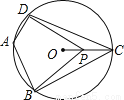
��ͼ���ı���ABCD�ڽ��ڡ�O����DAB=120�㣬����OC����P�ǰ뾶OC������һ�㣬����DP��BP�����BPD����Ϊ______�ȣ�д��һ�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�п���ѧģ���Ծ� ���ͣ������
��֪����x�ķ���kx2+��2k+1��x+2=0��
��1����֤������kȡ�κ�ʵ��ʱ����������ʵ������
��2����������y=kx2+��2k+1��x+2ͼ����x����������ĺ������Ϊ��������kΪ������ʱ����P��a��y1����Q��1��y2���Ǵ��������ϵ����㣬��y1��y2�����Ϻ���ͼ��ȷ��ʵ��a��ȡֵ��Χ��
��3����֪������y=kx2+��2k+1��x+2������㣬����������꣮
��1��֤������������2��a��1��a����4����3�������ߺ�����㣨0��2��������2��0���� �������������������1���������ۣ��÷�����һԪһ�η��̺�һԪ���η���������������÷���ΪһԪ���η���ʱ�������б�ʽ����0����������ʵ������ ��2��ͨ����kx2+��2k+1��x+2=0�õ�k=1���ɴ˵õ��������߽���ʽΪy=x2+3x+2�����ͼ��ش����⣮ ��3����������õ�kx2+��2k+...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
��ʽ����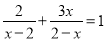 �Ľ�Ϊ��������
�Ľ�Ϊ��������
A. 1 B. 2 C. 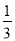 D. 0
D. 0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ����ˣ� ���ͣ������
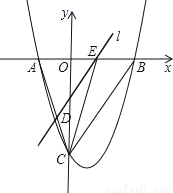
��ͼ��������y=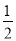 x2��
x2��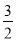 x��9��x�ύ��A��B���㣬��y�ύ�ڵ�C������BC��AC��
x��9��x�ύ��A��B���㣬��y�ύ�ڵ�C������BC��AC��
��1����AB��OC�ij���
��2����E�ӵ�A��������x�����B�˶�����E���A��B���غϣ�������E��ֱ��lƽ��BC����AC�ڵ�D����AE�ij�Ϊm����ADE�����Ϊs����s����m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3���ڣ�2���������£�����CE�����CDE��������ֵ����ʱ������Ե�EΪԲ�ģ���BC���е�Բ���������������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ����ˣ� ���ͣ������
��������y=x2-4x+5��ͼ������ƽ��3����λ��������ƽ��2����λ������ͼ��Ľ���ʽ��
y=x2-10x+24�� �������� ����������������䷽����������y=x2-4x+5д�ɶ���ʽ���ٸ��ݡ��ϼ��¼�������Ҽ�����ԭ����н�ɣ� ���������y=x2-4x+5=��x-2��2+1�� �ɡ�����Ҽ�����ԭ���֪��������y=��x-2��2+1��ͼ������ƽ��3����λ���ú���ͼ��Ĺ�ϵʽ�ǣ�y=��x-5��2+1�� �ɡ��ϼ��¼�����ԭ���֪��������y=��x-5��2+1��ͼ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ����ˣ� ���ͣ���ѡ��
��ͼ��P������A��0�� 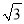 ����O��0��0����B��1��0������C�ڵ�һ����
����O��0��0����B��1��0������C�ڵ�һ����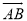 �ϣ����BCO�Ķ���Ϊ��������
�ϣ����BCO�Ķ���Ϊ��������
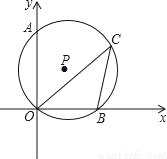
A. 15�� B. 30�� C. 45�� D. 60��
B ���������������������AB�� ��tan��OAB=�� ���OAB=30�㣬 ���OCB=��OAB=30�㣨Բ�ܽǶ������� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ�������п���ѧ��ģ�Ծ���һ�� ���ͣ������
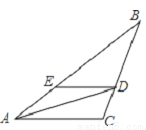
��ͼ���ڡ�ABC�У�ADƽ�֡�BAC����BC�ߵĽ���ΪD����DC= BC��DE��AC����AB�ߵĽ���ΪE����DE=4����BE�ij�Ϊ__________����
BC��DE��AC����AB�ߵĽ���ΪE����DE=4����BE�ij�Ϊ__________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
�����ڱ߷ֱ���ȵ��ı��ν��������Ρ�����ͼ���ı���ABCD��һ�����Σ�����AD=CD��AB=CB����̽�����ε�����ʱ���õ����½��ۣ��١�ABD�ա�CBD����AC��BD�����ı���ABCD�����= AC•BD��������ȷ�Ľ����У� ��
AC•BD��������ȷ�Ľ����У� ��
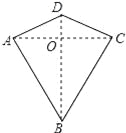
A. 0�� B. 1�� C. 2�� D. 3��
D ������������������ڡ�ABD���CBD�У� ���ɵá�ABD�ա�CBD��SSS�����ʢ���ȷ�� ����ȫ�������ε����ʣ��ɵá�ADB=��CDB���ڡ�AOD���COD�У� ���ɵá�AOD�ա�COD��SAS�����ɵá�AOD=��COD=90�㣬AO=OC�����ݴ�ֱ�Ķ���ɵ�AC��DB���ʢ���ȷ�� �ı���ABCD�����= =ACBD���ʢ���ȷ�� ��ѡD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com