练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    矩形具有而菱形不具有的性质是（　　）

    A. 对角线相等 B. 两组对边分别平行

    C. 对角线互相平分 D. 两组对角分别相等

    A 【解析】【解析】 ∵矩形具有的性质是：对角线相等且互相平分，两组对边分别平行，两组对角分别相等；菱形具有的性质是：两组对边分别平行，对角线互相平分，两组对角分别相等； ∴矩形具有而菱形不具有的性质是：对角线相等． 故选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年广东省八年级12月月考数学试卷 题型：填空题

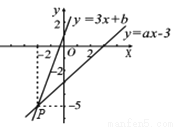
    如图，已知函数y＝3x＋b和y＝ax－3的图像交于点P(－2,－5)，则根据图像可得不等式ax－3＜3x＋b≤0的解集是___．

    -2＜x≤ 【解析】【解析】 ∵y=3x+b经过（﹣2，﹣5），∴﹣5=﹣6+b，解得：b=1，∴函数关系式为y=3x+1，当y=0时，3x+1=0，x=﹣，根据图象可得ax﹣3＜3x+b≤0的解集是﹣2＜x≤﹣，故答案为：﹣2＜x≤﹣．

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：解答题

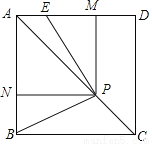
    如图，已知正方形ABCD，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB．

    （1）求证：四边形PMAN是正方形；

    （2）求证：EM=BN．

    （1）证明见解析；（2）证明见解析. 【解析】试题分析： （1）先证四边形PMAN是矩形，再证PM=PN； （2）用ASA证明△EPM≌△BPN. 试题解析： （1）证明：∵四边形ABCD是正方形，∴∠BAD=90°，AC平分∠BAD， ∵PM⊥AD，PN⊥AB，∴PM=PN，∠PMA=∠PNA=90°， ∴四边形PMAN是矩形， ∵PM=PN，∴四...

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：解答题

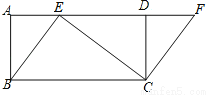
    如图，四边形ABCD是矩形，点E在AD边上，点F在AD的延长线上，且BE=CF．

    （1）求证：四边形EBCF是平行四边形．

    （2）若∠BEC=90°，∠ABE=30°，AB=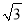，求ED的长．

    （1）证明见解析（2）3 【解析】试题分析： （1）由AB=CD，BE=CF，可证Rt△BAE≌Rt△CDF，从而证得BE∥CF，即可得证； （2）由题意可知∠2=30°，∠1=∠3=60°，在直角△ABE中求出AE，BE，在直角△BEC中求出BC的长，即可求出ED的长. 试题解析： （1）证明： ∵四边形ABCD是矩形，∴∠A=∠CDF=∠ABC=90°，AB...

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：填空题

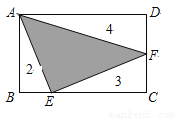
    如图，矩形ABCD被分成四部分，其中△ABE、△ECF、△ADF的面积分别为2、3、4，

    则△AEF的面积为______．

    7 【解析】试题解析：设AB=a，BC=b， ∵△CEF，△ABE，△ADF的面积分别是2，3，4， ∴S△ABE=×a×BE=2， ∴BE=， ∴EC=BC-BE=b-， ∵S△CEF=×EC×FC=3， ∴FC=， ∴DF=CD-CF=a-， ∴S△ADF=×（a-）×b=4， ∴（ab）2-18ab+32=0， 解得：ab=1...

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：单选题

    矩形具有而平行四边形不一定具有的性质是（　　）

    A. 对角相等 B. 对边相等

    C. 对角线相等 D. 对角线互相平分

    C 【解析】试题解析：矩形的 对角线相等，而平行四边形的对角线不一定相等. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：河北省沙河市2017-2018学年九年级上学期期末模拟联考数学试卷(冀教版) 题型：解答题

    如图，反比例函数y=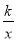（k≠0）的图象过等边三角形AOB的顶点A，已知点B（﹣2，0）

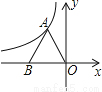
    （1）求反比例函数的表达式；

    （2）若要使点B在上述反比例函数的图象上，需将△ABC向上平移多少个单位长度？

    (1)y=-；(2) 【解析】试题分析：（1）首先过点A作AC⊥x轴于点C，由△AOB是等边三角形，B（﹣2，0），即可求得点A的坐标，继而求得反比例函数的表达式； （2）由当时， ，则可得要使点B在上述反比例函数的图象上，需将△ABC向上平移个单位长度． 试题解析：（1）过点A作AC⊥x轴于点C，∵△AOB是等边三角形，B（﹣2，0），∴OC=1，AC=， ∴点A的坐标为...

    查看答案和解析>>

    科目：初中数学 来源：河北省沙河市2017-2018学年九年级上学期期末模拟联考数学试卷(冀教版) 题型：单选题

    如图，矩形ABCD∽矩形AFEB，若S矩形ABCD：S矩形AFEB=9：16，AB=6，则S矩形ABCD的值为（）

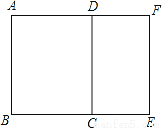
    A． 9 B． 16 C． 27 D． 48

    C. 【解析】 试题分析：先根据矩形ABCD∽矩形AFEB，若S矩形ABCD：S矩形AFEB=9：16得出的值，再由AB=6可求出AF的长，进而可得出结论． 解答：【解析】 ∵矩形ABCD∽矩形AFEB，S矩形ABCD：S矩形AFEB=9：16， ∴， ∵AB=6， ∴AF=8， ∴S矩形AFEBF=6×8=48， ∴S矩形ABCD=48×=27．...

    查看答案和解析>>

    科目：初中数学 来源：2018届中考数学一轮复习单元检测：第1讲 实数概念与运算 题型：单选题

    有理数a，b在数轴上对应点的位置如图所示，下列各式正确的是( )

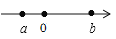
    A. a－b＜0 B. a＋b＜0

    C. a·b＞0 D. 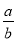＞0

    A 【解析】试题解析：由a，b在数轴上对应点的位置如图所示，得 a＜0＜b，|a|＜|b|， A、a-b＜0，故A符合题意； B、a+b＜0，故B不符合题意； C、a•b＞0，故C不符合题意； D、＜0，故D不符合题意. 故选A．

    查看答案和解析>>

    同步练习册答案