解:(1)∵抛物线与x轴交于A、B两点,对称轴为直线x=2,且A(1,0),
∴B(3,0),
∴可设抛物线的解析式为y=a(x-1)(x-3),
将C(0,-3)代入,得-3=3a,
解得:a=-1,
故抛物线的解析式为:y=-(x-1)(x-3),即y=-x
2+4x-3;
(2)①
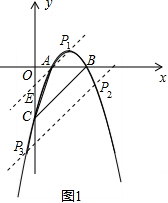
当△PBC面积与△ABC面积相等时,分两种情况:
(i)当点P在直线BC的上方时,如图1,过点A作直线BC的平行线交抛物线于点P
1.
设直线BC的解析式为y=kx+b.
∵B(3,0),C(0,-3),
∴

,解得

,
∴直线BC的解析式为y=x-3.
∴设直线AP
1的解析式为y=x+n.
∵直线AP
1过点A(1,0),
∴1+n=0,解得n=-1.
∴直线AP
1的解析式为y=x-1.
解方程组
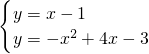
,得
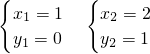
,
∴点P
1的坐标为(2,1);
(ii)当点P在直线BC的下方时,如图1.
设直线AP
1交y轴于点E,则E点坐标为(0,-1).
把直线BC向下平移2个单位,交抛物线于点P
2、P
3,得直线P
2P
3的解析式为y=x-5.
解方程组
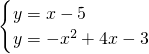
,得
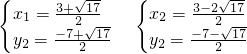
,
∴P
2的坐标为(

,
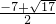
),P
3的坐标为(

,
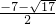
);
综上所述,点P坐标为:P
1(2,1),P
2(

,
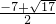
),P
3(

,
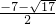
);
②∵B(3,0),C(0,-3),
∴OB=OC=3,
∴∠OCB=∠OBC=45°.
设直线CP的解析式为y=mx-3.
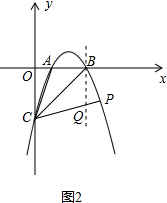
如图2,过点B作x轴的垂线,交CP于点Q.
∵∠ABC=45°,
∴∠CBQ=45°,
∴∠ABC=∠QBC,
又∵∠ACB=∠QCB,BC=BC,
∴△CAB≌△CQB,
∴AB=BQ=2,
∴点Q的坐标为(3,-2).
∵直线CP过点Q(3,-2),
∴3m-3=-2,解得m=

.
∴直线CP的解析式为y=

x-3.
分析:(1)先由抛物线的对称轴为直线x=2,且过点A(1,0),根据抛物线的对称性得B的坐标为(3,0),则可设抛物线的解析式为y=a(x-1)(x-3),再将C(0,-3)代入,可解得:a=-1,进而求出抛物线的解析式;
(2)①由于同底等高的两个三角形面积相等,所以当△PBC面积与△ABC面积相等时,将BC看作是底,那么这两个三角形BC边上的高相等.由于到一条直线距离相等的直线有两条,所以分两种情况进行讨论:(i)当点P在直线BC的上方时,过点A作直线BC的平行线交抛物线于点P
1,先运用待定系数法求出直线BC的解析式,则直线AP
1的比例系数与直线BC的比例系数相同,又直线AP
1过点A(1,0),运用待定系数法求出直线AP
1的解析式,再将它与抛物线的解析式联立,组成方程组,解方程组求出点P
1的坐标;(ii)当点P在直线BC的下方时,设直线AP
1交y轴于点E,则E点坐标为(0,-1),由于直线AP
1与直线BC的距离等于直线P
2P
3与直线BC的距离,所以容易求出直线P
2P
3的解析式,再将它与抛物线的解析式联立,组成方程组,解方程组求出点P
2、P
3的坐标;
②先由B、C两点的坐标可知OB=OC=3,则∠OCB=∠OBC=45°.设直线CP的解析式为y=mx-3.过点B作x轴的垂线,交CP于点Q,利用ASA证明△CAB≌△CQB,则AB=BQ=2,得到点Q的坐标为(3,-2),将它代入y=mx-3,运用待定系数法即可求出直线CP的解析式.
点评:本题是二次函数的综合题型,其中涉及到的知识点有运用待定系数法求一次函数、二次函数的解析式,三角形的面积,两函数交点坐标的求法,全等三角形的判定与性质,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.


 当△PBC面积与△ABC面积相等时,分两种情况:
当△PBC面积与△ABC面积相等时,分两种情况: ,解得
,解得 ,
,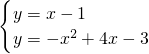 ,得
,得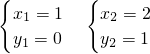 ,
,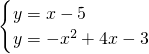 ,得
,得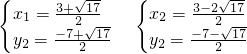 ,
, ,
,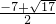 ),P3的坐标为(
),P3的坐标为( ,
,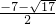 );
); ,
,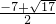 ),P3(
),P3( ,
,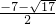 );
); ②∵B(3,0),C(0,-3),
②∵B(3,0),C(0,-3), .
. x-3.
x-3.

 如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).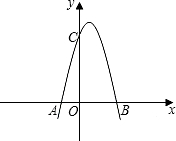 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8). 如图,已知抛物线与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,3). (2012•岳阳一模)如图,已知抛物线与x轴交于A(-4,0)和B(1,0)两点,与y轴交于C(0,-2)点.
(2012•岳阳一模)如图,已知抛物线与x轴交于A(-4,0)和B(1,0)两点,与y轴交于C(0,-2)点.