
 =________.
=________. 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
| 编号 | 20003 | 20008 | 20012 | 20016 | 20024 | 20028 | 20042 | 20048 | 20068 | 20075 |
| 馆别 | A | D | A | B | C | A | A | B | A | B |
| 编号 | 20079 | 20088 | 20091 | 20104 | 20116 | 20118 | 20122 | 20136 | 20144 | 20154 |
| 馆别 | A | B | C | A | A | B | A | D | A | B |
| 编号 | 20155 | 20163 | 20172 | 20188 | 20193 | 20199 | 20201 | 20208 | 20210 | 20229 |
| 馆别 | C | B | A | B | A | D | A | B | A | A |
| 编号 | 20235 | 20242 | 20253 | 20260 | 20264 | 20272 | 20284 | 20288 | 20294 | 20302 |
| 馆别 | A | C | A | D | A | B | A | C | A | D |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 编号 | 20003 | 20008 | 20012 | 20016 | 20024 | 20028 | 20042 | 20048 | 20068 | 20075 |
| 游戏 | A | D | A | B | C | A | A | B | A | B |
| 编号 | 20079 | 20088 | 20091 | 20104 | 20116 | 20118 | 20122 | 20136 | 20144 | 20154 |
| 游戏 | A | B | C | A | A | B | A | D | A | B |
| 编号 | 20155 | 20163 | 20172 | 20188 | 20193 | 20199 | 20201 | 20208 | 20210 | 20229 |
| 游戏 | C | B | A | B | A | D | A | B | A | A |
| 编号 | 20235 | 20242 | 20253 | 20260 | 20264 | 20272 | 20284 | 20288 | 20294 | 20302 |
| 游戏 | A | C | A | D | A | B | A | C | A | D |
查看答案和解析>>
科目:初中数学 来源: 题型:
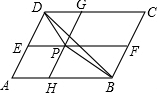 (1)已知|2011-x|+
(1)已知|2011-x|+| x-2012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com