
先化简,再求值:a3·(-b3)2+(-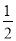 ab2)3,其中a=
ab2)3,其中a=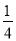 ,b=4.
,b=4.
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:单选题
如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )

A. 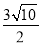 B.
B. 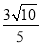 C.
C. 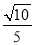 D.
D. 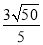
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市、吴江、相城七年级第一学期期末数学统考试卷 题型:解答题
先化简,再求值: 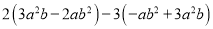 ,其中
,其中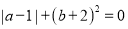 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市、吴江、相城七年级第一学期期末数学统考试卷 题型:单选题
下列图形中,不能折叠成一个正方体的是()
A. 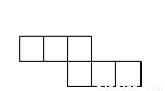 B.
B. 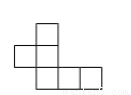 C.
C. 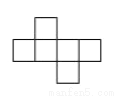 D.
D. 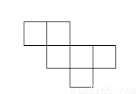
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
从扬州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为60km/h,B车的平均速度为A车的1.5倍,且走完全程B车所需时间比A车少45分钟.
(1)求扬州至南京的铁路里程;
(2)若两车以各自的平均速度分别从扬州、南京同时相向而行,问经过多少时间两车相距15km?
(1)135km;(2)0.8或1小时. 【解析】试题分析:(1)设扬州至南京的铁路里程是x km,依题意得到B车的平均速度为1.5xkm/h,根据走完全程B车所需时间比A车少45分钟,可列出方程求出解. (2)需要分类讨论:①相遇前相距两车相距15km;②相遇后两车相距15km. 试题解析:(1)设扬州至南京的铁路里程是x km,则 解得:x=135. 答:扬州至南...查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如图,直线AB、CD相交于点O,∠AOC=70°,∠BOE=25°,则∠DOE=______
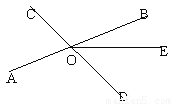
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
已知∠AOB=30°,又自∠AOB的顶点O引射线OC.若∠AOC:∠AOB=4:3,那么∠BOC= ( )
A. 10° B. 40° C. 45° D. 70°或10°
D 【解析】试题解析:∵∠AOB=30°,∠AOC:∠AOB=4:3, ∴∠AOC=40° 当OC在OA的外侧时,∠BOC=∠AOC+∠AOB=40°+30°=70°; 当OC在OB的外侧,∠BOC=∠AOC-∠AOB=40°-30°=10°. 故选D.查看答案和解析>>
科目:初中数学 来源:河北省保定市高阳县2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
轮船沿江从P港顺流行驶到Q港,比从Q港返回P港少用3小时,若船速为26千米/时,水速为2千米/时,求P港和Q港相距多少千米.设P港和Q港相距x千米.根据题意,可列出的方程是______________.
【解析】解:设港和港相距千米, 由题意得: ,即, 故答案为: .查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷(解析版) 题型:解答题
如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.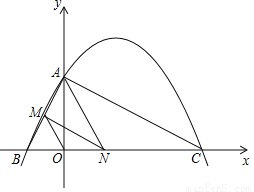
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com