
分析 ①根据直线解析式求得直线与坐标轴的交点,进而运用面积法求得原点到l的距离;
②当m=-1时,直线l为y=-x+n-1,求得与y轴交于(0,n-1),再根据l与直线l1的交点在第二象限,即可得出n-1的范围是-2<n-1<4,进而得到n的范围;
③当m=n时,直线l为y=mx+m-1,求得当x=-1时,y=-m+m-1=-1,进而得到直线l经过定点(-1,-1);
④当m=n<0时,直线l与x轴交于负半轴上的A点,求得当y=0时,0=mx+n-1,解得x=$\frac{1-n}{m}$,进而得到当m=n时,x=$\frac{1}{m}$-1,再根据m<0,得到$\frac{1}{m}$-1<-1,即点A离原点的距离大于1,即可得出OA的长度始终大于1.
解答 解:①当n=5,m=-$\frac{4}{3}$时,直线l为:y=-$\frac{4}{3}$x+4,
∴直线l与坐标轴分别交于(3,0)和(0,4),
∴原点到l的距离为$\frac{12}{5}$,故结论①错误;
②当m=-1时,直线l为y=-x+n-1,与y轴交于(0,n-1),
直线l1:y=2x+4与坐标轴交于(-2,0),(0,4),
∵l与直线l1的交点在第二象限,
∴n-1的范围是:-2<n-1<4,
∴n的范围为-1<n<5,故结论②错误;
③当m=n时,直线l为y=mx+m-1,
∴当x=-1时,y=-m+m-1=-1,
∴直线l经过定点(-1,-1),故结论③错误;
④当m=n<0时,直线1经过第二三四象限,
∴直线l与x轴交于负半轴上的A点,
∴当y=0时,0=mx+n-1,
解得x=$\frac{1-n}{m}$,
当m=n时,x=$\frac{1}{m}$-1,
又∵m<0,
∴$\frac{1}{m}$-1<-1,即点A离原点的距离大于1,
∴OA的长度始终大于1,故结论④正确.
综上所述,①②③错误,④正确.
点评 本题属于两直线相交或平行的问题,解决问题的关键是掌握一次函数的图象与性质,解题时注意:一次函数y=kx+b(k≠0,且k,b为常数)的图象是一条直线,与x轴的交点坐标是(-$\frac{b}{k}$,0),与y轴的交点坐标是(0,b).


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:选择题
| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AD∥BC | D. | ∠A=∠C,∠B=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
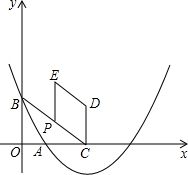 如图在平面直角坐标系xOy中,抛物线y=$\frac{\sqrt{3}}{5}{x}^{2}$+bx+c过点A(1,0),B(0,$\sqrt{3}$),这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),射线PC绕点P逆时针旋转120°,得线段PE,作平行四边形PCDE.
如图在平面直角坐标系xOy中,抛物线y=$\frac{\sqrt{3}}{5}{x}^{2}$+bx+c过点A(1,0),B(0,$\sqrt{3}$),这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),射线PC绕点P逆时针旋转120°,得线段PE,作平行四边形PCDE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com