
点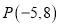 关于
关于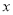 轴的对称点在( ).
轴的对称点在( ).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C 【解析】∵点P(-5,8)在第二象限, ∴点P关于x 的对称点在第三象限. 故选C. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:单选题
下列世界博览会会徽图案中是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学模拟试卷 题型:单选题
一个几何体的三视图如图所示,这个几何体是( )
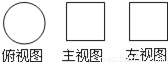
A. 棱柱 B. 正方形 C. 圆柱 D. 圆锥
C 【解析】试题解析:根据主视图和左视图为矩形可判断出该几何体是柱体, 根据俯视图是圆可判断出该几何体为圆柱. 故选C.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:填空题
不等式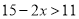 的正整数解为__________.
的正整数解为__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
已知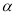 是等边三角形的一个内角,
是等边三角形的一个内角, 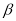 是顶角为
是顶角为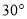 的等腰三角形的一个底角,
的等腰三角形的一个底角, 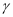 是等腰直角三角形的一个底角,则( ).
是等腰直角三角形的一个底角,则( ).
A. 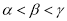 B.
B. 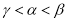 C.
C. 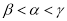 D.
D. 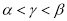
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
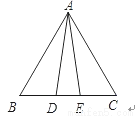
已知:如图,D、E是△ABC中BC边上的两点,AD=AE,要证明△ABE≌△ACD,应该再增加一个什么条件?请你增加这个条件后再给予证明.
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
一个大的等腰三角形能被分割为两个小等腰三角形,则该大等腰三角形顶角的度数是________.
108°或90°或36°或 【解析】因为题中没有指明这个等腰三角形是什么形状,故应该分四种情况进行分析,从而得到: (1)如图1,△ABC中,AB=AC,BD=AD,AC=CD,求∠BAC的度数. ∵AB=AC,BD=AD,AC=CD, ∴∠B=∠C=∠BAD,∠CDA=∠CAD, ∵∠CDA=2∠B, ∴∠CAB=3∠B, ∵∠BAC+∠B+∠C=180...查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
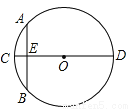
“圆材埋壁”是我国古代著名的数学著作《九章算数》中的一个问题,”今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何? 用现在的数学语言表述是:如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”.
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年八年级上学期期中联考数学试卷 题型:解答题
如图,AB为一棵大树(垂直于地面,即AB⊥BC),在树上距地面12m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处向上爬到树顶A处,再利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子经过的路程都是20m,求树高AB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com